Arithmagons Poster

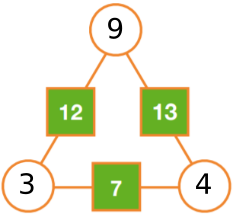
The numbers in the squares are the sum of the numbers in the circles on either side:

8 = 2 + 6

9 = 2 + 7

13 = 6 + 7

How to work out the numbers in the circles from the numbers in the squares

Method 1 - differences

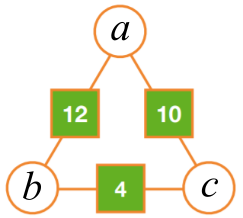Suppose the numbers in the circles are $a$, $b$ and $c$.

$a +b = 12$

$a + c = 10$

So $b$ is $2$ more than $c,$ so $b = c+2$

$b+c=4,$ so $(c+2)+c = 4$

$\Rightarrow 2c + 2 = 4 \Rightarrow c=1$

$a + c = 10$ so $a=9$

$b+c=4$ so $b=3$

Method 2 - sums

$a+b=12, a+c=10, b+c=4$

Add everything: $a+b+a+c+b+c = 12+10+4 \Rightarrow 2a+2b+2c = 26$

$2a + 2(b+c) = 26\Rightarrow 2a + 2\times 4 = 26\Rightarrow 2a = 26-2\times4\Rightarrow a = 9$

Similarly $2b + 2\times20 = 26 \Rightarrow b = 3$

And $2c + 2\times12 = 26 \Rightarrow c = 1$

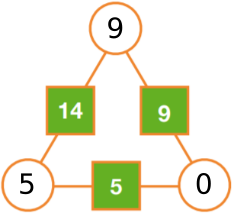
Using either of these methods, the missing numbers on the other arithmagons on the poster are: