Right Angles
Samantha and Shummus both realised that in order to create a triangle with a right angle, the band had to go through the centre of the circle. Shummus writes:
I noticed that the bands had to be started in the centre.Xianglong Ni notes that:
If we have 9 points on the circle then you can't create a right-angle using the points. This is so because a right angle is inscribed in a semicircle; It is facing a diameter. But you can only create a diameter when there is an even amount of points on the circle. If the number of points on the circle is even then yes. If the number is odd then no.
Rachel from Newstead sent us a few diagrams to illustrate examples of right-angled triangles in circles with an even number of points.
If you haven't met this idea before, you may want to look at another problem from August 2005, Subtended angles
Here are another couple of examples of right-angled triangles using the same eight-point and ten-point circles that Rachel used:
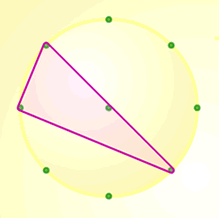
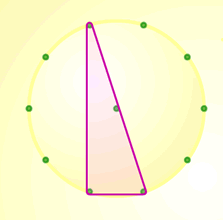
You may also like
Coins on a Plate
Points A, B and C are the centres of three circles, each one of which touches the other two. Prove that the perimeter of the triangle ABC is equal to the diameter of the largest circle.
Not So Little X
Two circles are enclosed by a rectangle 12 units by x units. The distance between the centres of the two circles is x/3 units. How big is x?
The Cyclic Quadrilateral
This gives a short summary of the properties and theorems of cyclic quadrilaterals and links to some practical examples to be found elsewhere on the site.