Skip over navigation
Twisting has the effect of adding 1: $$x \mapsto x+1$$
Turning transforms any number into the negative of its reciprocal: $$x \mapsto -\frac1x$$
You may wish to pause the video at each stage and invite students to work out what the next fraction will be. Below is a useful table showing the operation and the fraction at each stage of the video.
If students have grasped the two operations, you could challenge them to work out a sequence of twists and turns to get back from $-\frac5{13}$ to $0$. Alternatively, watch the rest of the video to see the surprising moment when the ropes disentangle. Here is the sequence:
Now that students understand the two operations, set them the challenge in the problem - working out the fraction for each stage of the sequence, and working out the sequence to get back to zero:
To finish off, students could perform their sequence to tangle and untangle their own set of skipping ropes, before moving on to More Twisting and Turning. Alternatively, they could perform the sequence individually using string and card, as shown below.

What fraction do you reach next if you turn?
How will you decide whether to twist or turn next?

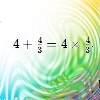
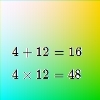
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Twisting and Turning
Age 11 to 14
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Why do this problem?
This problem introduces an intriguing trick which provides a context for practising manipulation of fractions. Watching the video, or perhaps trying the trick out for themselves, can engage students' curiosity, and lead to some intriguing mathematics to explore and explain.Possible approach
Show the video in the problem, and explain the two functions:Twisting has the effect of adding 1: $$x \mapsto x+1$$
Turning transforms any number into the negative of its reciprocal: $$x \mapsto -\frac1x$$
You may wish to pause the video at each stage and invite students to work out what the next fraction will be. Below is a useful table showing the operation and the fraction at each stage of the video.
| Operation | Fraction |
|---|---|
| Twist | $1$ |
| Twist | $2$ |
| Turn | $-\frac12$ |
| Twist | $\frac12$ |
| Twist | $1\frac12$, or $\frac32$ |
| Twist | $2\frac12$, or $\frac52$ |
| Turn | $-\frac25$ |
| Twist | $\frac35$ |
| Twist | $1\frac35$, or $\frac85$ |
| Twist | $2\frac35$, or $\frac{13}5$ |
| Turn | $-\frac5{13}$ |
If students have grasped the two operations, you could challenge them to work out a sequence of twists and turns to get back from $-\frac5{13}$ to $0$. Alternatively, watch the rest of the video to see the surprising moment when the ropes disentangle. Here is the sequence:
| Operation | Fraction |
|---|---|
| Twist | $\frac8{13}$ |
| Turn | $-\frac{13}8$ or $-1\frac58$ |
| Twist | $-\frac58$ |
| Twist | $\frac38$ |
| Turn | $-\frac83$ or $-2\frac23$ |
| Twist | $-\frac53$ or $-1\frac23$ |
| Twist | $-\frac23$ |
| Twist | $\frac13$ |
| Turn | $-3$ |
| Twist | $-2$ |
| Twist | $-1$ |
| Twist | $0$ |
Now that students understand the two operations, set them the challenge in the problem - working out the fraction for each stage of the sequence, and working out the sequence to get back to zero:
Twist, twist, twist, turn, twist, twist, twist, turn, twist, twist, twist, turn
To finish off, students could perform their sequence to tangle and untangle their own set of skipping ropes, before moving on to More Twisting and Turning. Alternatively, they could perform the sequence individually using string and card, as shown below.

Key questions
What fraction do you reach next if you twist?What fraction do you reach next if you turn?
How will you decide whether to twist or turn next?
Possible extension
This is the first of three related problems. The second problem is More Twisting and Turning and the third is All Tangled Up.Possible support
For a more structured opportunity to practise operations with fractions, see Peaches Today, Peaches Tomorrow...Related Collections
You may also like
Tweedle Dum and Tweedle Dee
Two brothers were left some money, amounting to an exact number of pounds, to divide between them. DEE undertook the division. "But your heap is larger than mine!" cried DUM...
Sum Equals Product
The sum of the numbers 4 and 1 [1/3] is the same as the product of 4 and 1 [1/3]; that is to say 4 + 1 [1/3] = 4 � 1 [1/3]. What other numbers have the sum equal to the product and can this be so for any whole numbers?
Special Sums and Products
Find some examples of pairs of numbers such that their sum is a factor of their product. eg. 4 + 12 = 16 and 4 × 12 = 48 and 16 is a factor of 48.

