Skip over navigation
For it to be possible to draw a figure without taking the pen off the paper and without drawing along an existing line, there must be either no points or exactly two points in the figure at which an odd number of lines meet.
To see why this must be the case, let us consider one point where lines meet and let us also suppose that we neither start nor end to draw the figure at that point. Since we are not allowed to draw along an existing line and as we 'enter' such a point from one direction, we need to leave it along a different line. So an even number of lines meet at such a point.
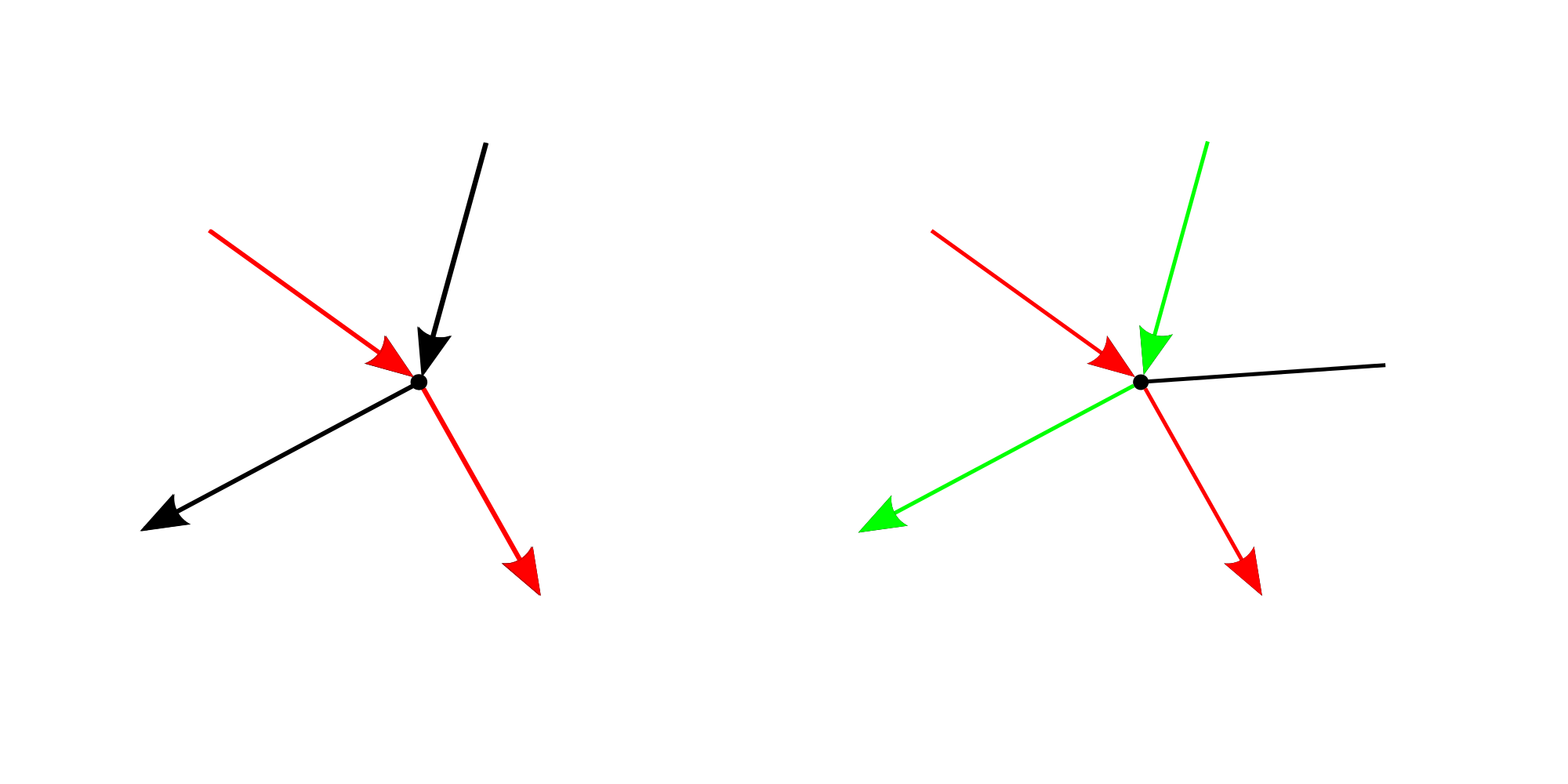
If the starting and the end point coincide then this is also a point at which an even number of lines meet. Otherwise, both the starting and the end point are points at which an odd number of lines meet as we leave (enter) this point once without entering (leaving) the point.
We can now check that only the last picture satisfies these conditions and indeed, one can draw it without taking the pen off the paper and without drawing along an existing line.
Eulerian
Age 14 to 16
ShortChallenge Level 
For it to be possible to draw a figure without taking the pen off the paper and without drawing along an existing line, there must be either no points or exactly two points in the figure at which an odd number of lines meet.
To see why this must be the case, let us consider one point where lines meet and let us also suppose that we neither start nor end to draw the figure at that point. Since we are not allowed to draw along an existing line and as we 'enter' such a point from one direction, we need to leave it along a different line. So an even number of lines meet at such a point.
If the starting and the end point coincide then this is also a point at which an even number of lines meet. Otherwise, both the starting and the end point are points at which an odd number of lines meet as we leave (enter) this point once without entering (leaving) the point.
We can now check that only the last picture satisfies these conditions and indeed, one can draw it without taking the pen off the paper and without drawing along an existing line.
This problem is taken from the UKMT Mathematical Challenges.
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Polycircles
Show that for any triangle it is always possible to construct 3 touching circles with centres at the vertices. Is it possible to construct touching circles centred at the vertices of any polygon?
Pick's Theorem
Polygons drawn on square dotty paper have dots on their perimeter (p) and often internal (i) ones as well. Find a relationship between p, i and the area of the polygons.
Producing an Integer
Multiply a sequence of n terms together. Can you work out when this product is equal to an integer?