Skip over navigation
Answer: 7 girls
$b$ boys and $g$ girls, so $\frac{b+g}{3}$ teddy bears.
Books taken out: $$\begin{align}12b+17g+9\times\tfrac{b+g}{3}&=305\\
\Rightarrow 12b+17g+3(b+g)&=305\\ \Rightarrow15b+20g&=305\end{align}$$
Divide through by $5$: $$3b+4g=61$$ $b$ and $g$ must be whole numbers
Also need the number of teddy bears to be an integer so the total number of students is a multiple of $3$
$3+13=16$ no
$7 + 10 = 17$ no
$11 +7=18$ yes
$15+4=19$ no
$19+1=20$ no
So the number of girls is $7$.

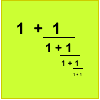
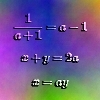
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Well Read
Age 14 to 16
ShortChallenge Level 





- Problem
- Solutions
Answer: 7 girls
$b$ boys and $g$ girls, so $\frac{b+g}{3}$ teddy bears.
Books taken out: $$\begin{align}12b+17g+9\times\tfrac{b+g}{3}&=305\\
\Rightarrow 12b+17g+3(b+g)&=305\\ \Rightarrow15b+20g&=305\end{align}$$
Divide through by $5$: $$3b+4g=61$$ $b$ and $g$ must be whole numbers
| $3b$ | $61-3b$ | Divisible by $4$? |
| $3$ | $58$ | no |
| $6$ | $55$ | no |
| even multiples of $3$ give odd numbers so only try odd multiples of $3$ |
||
| $9$ | $52$ | yes, $4\times13$; $3$ boys and $13$ girls |
| $15$ | $46$ | no |
| $21$ | $40$ | yes, $4\times10$; $7$ boys and $10$ girls |
| $27$ | $34$ | no |
| go up/down in $12$s (multiple of $4$) not $6$s to hit the multiples of $4$ |
||
| $33$ | $28$ | yes, $4\times7$; $11$ boys and $7$ girls |
| $45$ | $16$ | yes, $4\times4$; $15$ boys and $4$ girls |
| $57$ | $4$ | yes, $4\times1$; $19$ boys and $1$ girl |
Also need the number of teddy bears to be an integer so the total number of students is a multiple of $3$
$3+13=16$ no
$7 + 10 = 17$ no
$11 +7=18$ yes
$15+4=19$ no
$19+1=20$ no
So the number of girls is $7$.
This problem is taken from the UKMT Mathematical Challenges.
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Always Two
Find all the triples of numbers a, b, c such that each one of them plus the product of the other two is always 2.
Not Continued Fractions
Which rational numbers cannot be written in the form x + 1/(y + 1/z) where x, y and z are integers?
Surds
Find the exact values of x, y and a satisfying the following system of equations: 1/(a+1) = a - 1 x + y = 2a x = ay

