Bugs in the Garden

From Jacob, Luc and William at The Hall School in London we had the following, very thorough solution sent in, 

We looked at the number of spots that could be produced when you have a four spotted bug or a seven spotted bug or a combination of both.
We were asked if it was possible to make $16$ and we found it is, by using four of the four spotted bugs. We discovered that the smallest number of spots we could produce was $4$.
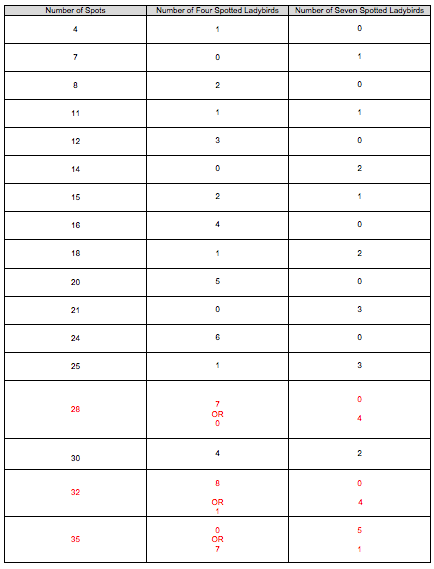
We were then asked what number of spots between $4$ and $35$ could be produced. We started off by writing a list of those numbers that did and didn't work. Then we made a table to show how we made the numbers of spots that were possible.
We found seventeen different numbers could be made and three that could be made in two different ways. These were $28, 32$ and $35$.
We have drawn a table to show the only number of spots that can be made between $4$ and $35$. For each number of spots that it is possible to make we have shown the number of four spotted and seven spotted bugs that make up the number of spots.

We also had some ideas sent in from Christian at Heronsgate School, Olivia from Risley Lower Primary School both in England. From Australia we had a solution sent in from Maths Group $2$ at Brunswick South Primary School.
Well done everyone!