Spiralling Decimals
Have you noticed that some very long numbers are very big whilst other very long numbers are small? Can you think of an example of each?
Here's a game where you can test your skill at putting small numbers into the right order - it's not as easy as it sounds!
How to play
You need a partner, a copy of the game board, and two different coloured pencils.
Decide who goes first.
Take turns to choose a number from the grid and mark it on the spiral. Make sure you know where 0 and where 1 is!
Keep taking turns until one of you has marked three numbers next to each other.
| 0.5 | 0.25 | 0.75 | 0.3 |
| 0.35 | 0.9 | 0.99 | 0.999 |
| 0.1 | 0.01 | 0.05 | 0.79 |
| 0.64 | 0.32 | 0.54 | 0.865 |
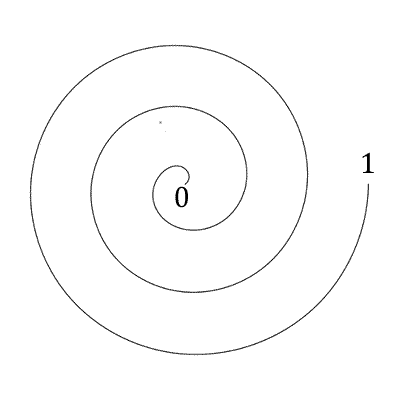
What next?
Can you work out a winning strategy?
Does it matter who goes first?
Does it matter which number you choose first?
Can you make up a different set of numbers which would make the game more challenging?
Perhaps you could have different start and end numbers for your spiral?
Send us your ideas so that we can share them with other children.
You may be interested in the other problems in our Fractions Unpacked Feature.
You may also like
Pebbles
Place four pebbles on the sand in the form of a square. Keep adding as few pebbles as necessary to double the area. How many extra pebbles are added each time?
Bracelets
Investigate the different shaped bracelets you could make from 18 different spherical beads. How do they compare if you use 24 beads?
Sweets in a Box
How many different shaped boxes can you design for 36 sweets in one layer? Can you arrange the sweets so that no sweets of the same colour are next to each other in any direction?