Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Spiralling Decimals



- Game
- Teachers' Resources
Spiralling Decimals
Have you noticed that some very long numbers are very big whilst other very long numbers are small? Can you think of an example of each?
Here's a game where you can test your skill at putting small numbers into the right order - it's not as easy as it sounds!
How to play
You need a partner, a copy of the game board, and two different coloured pencils.
Decide who goes first.
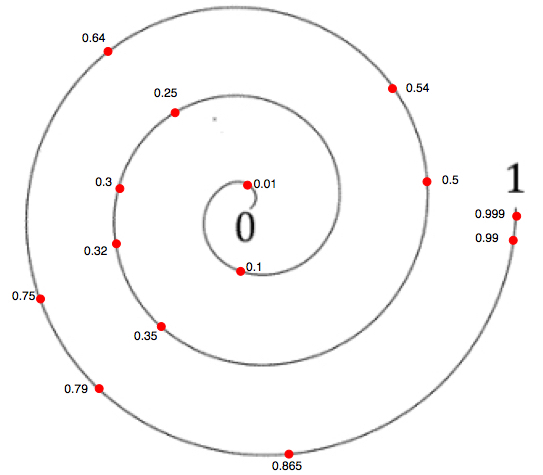
Take turns to choose a number from the grid and mark it on the spiral. Make sure you know where 0 and where 1 is!
Keep taking turns until one of you has marked three numbers next to each other.
| 0.5 | 0.25 | 0.75 | 0.3 |
| 0.35 | 0.9 | 0.99 | 0.999 |
| 0.1 | 0.01 | 0.05 | 1.79 |
| 0.64 | 0.32 | 0.54 | 0.865 |
Can you work out a winning strategy?
Does it matter who goes first?
Does it matter which number you choose first?
Can you make up a different set of numbers which would make the game more challenging?
Perhaps you could have different start and end numbers for your spiral?
Send us your ideas so that we can share them with other children.
Why play this game?
Ordering decimal numbers, especially those between 0 and 1, can be quite tricky especially if children hold the common misconception that the longer a number, the bigger it is. By placing numbers on a spiral rather than a straight line, children are helped to focus on the order of the numbers, ie their relative positions, rather than trying to work out their size. The game element means they practise a very large number of comparisons, whilst the more confident players can focus on trying to develop a winning strategy.Possible approach
Draw a large spiral on the white board, marking 0 in the middle and 1 on the outside. Ask a willing child to come and mark where they think 0.5 might be. Discuss how the spiral makes it difficult to know exactly where to put it, but that's not important - what matters here is that 0.5 is somewhere reasonably near the middle of 0 and 1.Ask another child to give a decimal number between 0 and 1 and, with the class, decide where this should be marked. Is it between 0 and 0.5, or between 0.5 and 1? Repeat with a few other decimals, modelling some which are very close and have different numbers of decimal places, e.g. 0.6 and 0.63. Develop some useful questions together - for example, 'is it bigger than...?'; 'is it smaller than...?'.
Explain that they are now going to play a game with a partner, where they take turns to choose from a set of numbers to place one on the spiral. The winner is the first player to mark three numbers consecutively. Different coloured pens can be helpful here. Give out the game boards.
Once everyone has had some time to play, bring the group back together and ask what they found easy and what they found difficult. Did they think it was a good game? Why? Invite them to design a different group of numbers that they think will improve the game. Allow time for them to play their new game and then bring the class together for feedback. You could collect good sets of numbers and display them as a challenge for the class to use when playing the game in their own time.
Key questions
Where will you place this number?This number is really long. Where does it go?
How do you know it goes there?
Is there a number you could place between these two?
Can you think of a better set of numbers?
Possible extension
Given free rein, you may be surprised at the numbers children choose for their own games. For a really difficult variation, and for children who are confident with negative numbers, try a spiral from -1 to 1.You could challenge children to create a number line on a strip of paper with all the numbers in the game marked on accurately, then to roll up the paper into a spiral shape to see where they actually appear. Here is a photo of just that, along with a computer-generated image of the result, which we found rather fascinating:

Possible support
Use the game board B which uses numbers with one decimal place and a spiral from 0 to 2.You may also like
Pebbles
Place four pebbles on the sand in the form of a square. Keep adding as few pebbles as necessary to double the area. How many extra pebbles are added each time?
Bracelets
Investigate the different shaped bracelets you could make from 18 different spherical beads. How do they compare if you use 24 beads?
Sweets in a Box
How many different shaped boxes can you design for 36 sweets in one layer? Can you arrange the sweets so that no sweets of the same colour are next to each other in any direction?

