Skip over navigation
Dicey Perimeter, Dicey Area
Age 7 to 11
Challenge Level 
This is a game for two players.
You will need two dice, some sheets of centimetre squared paper and two pencils or pens.
The aim of the game is to be the first to reach the agreed score.
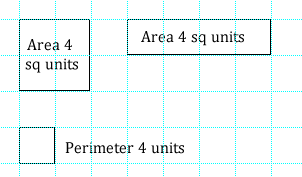How to play:
1. Decide on your target score. 10 might be a good number.
2. Decide who will go first.
3. Player 1 throws the two dice and finds their product.
4. Player 1 must then draw as many rectilinear* shapes as possible which have either an area or a perimeter equal to the product of the dice. Player 1 scores 1 point for each correct shape.
5. Player 2 throws the dice, finds their product and draws as many shapes as possible in the same way.
6. The winner of the game is the first to reach the agreed target score.
What are good numbers to throw? Why?
What are not very good numbers to throw? Why?
Is it better to go first or second or doesn't it matter?
*A rectilinear shape is one whose edges meet at right angles. In other words, if you are drawing your shapes on centimetre squared paper, the sides of the shape will always be on the grid lines, not drawn diagonally.
You will need two dice, some sheets of centimetre squared paper and two pencils or pens.
The aim of the game is to be the first to reach the agreed score.
How to play:1. Decide on your target score. 10 might be a good number.
2. Decide who will go first.
3. Player 1 throws the two dice and finds their product.
4. Player 1 must then draw as many rectilinear* shapes as possible which have either an area or a perimeter equal to the product of the dice. Player 1 scores 1 point for each correct shape.
5. Player 2 throws the dice, finds their product and draws as many shapes as possible in the same way.
6. The winner of the game is the first to reach the agreed target score.
What are good numbers to throw? Why?
What are not very good numbers to throw? Why?
Is it better to go first or second or doesn't it matter?
*A rectilinear shape is one whose edges meet at right angles. In other words, if you are drawing your shapes on centimetre squared paper, the sides of the shape will always be on the grid lines, not drawn diagonally.
You may also like
Geoboards
This practical challenge invites you to investigate the different squares you can make on a square geoboard or pegboard.
Tiles on a Patio
How many ways can you find of tiling the square patio, using square tiles of different sizes?
Pebbles
Place four pebbles on the sand in the form of a square. Keep adding as few pebbles as necessary to double the area. How many extra pebbles are added each time?