Skip over navigation
This is a game for two players.
You will need two dice, some sheets of centimetre squared paper and two pencils or pens.
The aim of the game is to be the first to reach the agreed score.
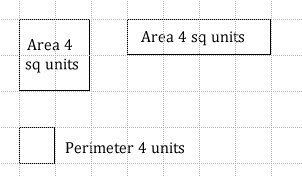How to play:
1. Decide on your target score. 10 might be a good number.
2. Decide who will go first.
3. Player 1 throws the two dice and finds their product.
4. Player 1 must then draw as many rectilinear* shapes as possible which have either an area or a perimeter equal to the product of the dice. Player 1 scores 1 point for each correct shape.
5. Player 2 throws the dice, finds their product and draws as many shapes as possible in the same way.
6. The winner of the game is the first to reach the agreed target score.
What are good numbers to throw? Why?
What are not very good numbers to throw? Why?
Is it better to go first or second or doesn't it matter?
*A rectilinear shape is one whose edges meet at right angles. In other words, if you are drawing your shapes on centimetre squared paper, the sides of the shape will always be on the grid lines, not drawn diagonally.
This activity will help learners become more familiar with the concepts of perimeter and area. It also encourages a systematic approach so that all possible shapes are found.
Throw the dice again and have another go. This time, once solutions have been shared, spend some time discussing ways of approaching the task, including ways of working systematically to ensure all possibilities have been found. You could make sure each child has laminated centimetre squared paper so that they can hold up their sheets. This means that everyone can see who has got the same shape and who has drawn something different. You could invite children to line up at the front of the room so that all the different shapes are displayed for a particular product. Can the class arrange them in an order? This will help them to understand what we mean by 'working systematically'.
You can then introduce the game aspect so that pairs can play against each other, perhaps with a target score of 10 at first.
Look out for children who are working systematically and those who have made connections. For example, once a shape has been found with a particular perimeter, some may notice that the same perimeter can be achieved by cutting out one or more corner squares.
Have you got all the shapes with that area/perimeter? How do you know?
How could you 'tweak' that shape to get another with the same perimeter?
Dicey Perimeter, Dicey Area
Age 7 to 11
Challenge Level 
Dicey Perimeter, Dicey Area
This is a game for two players.
You will need two dice, some sheets of centimetre squared paper and two pencils or pens.
The aim of the game is to be the first to reach the agreed score.
How to play:1. Decide on your target score. 10 might be a good number.
2. Decide who will go first.
3. Player 1 throws the two dice and finds their product.
4. Player 1 must then draw as many rectilinear* shapes as possible which have either an area or a perimeter equal to the product of the dice. Player 1 scores 1 point for each correct shape.
5. Player 2 throws the dice, finds their product and draws as many shapes as possible in the same way.
6. The winner of the game is the first to reach the agreed target score.
What are good numbers to throw? Why?
What are not very good numbers to throw? Why?
Is it better to go first or second or doesn't it matter?
*A rectilinear shape is one whose edges meet at right angles. In other words, if you are drawing your shapes on centimetre squared paper, the sides of the shape will always be on the grid lines, not drawn diagonally.
Why do this problem?
This activity will help learners become more familiar with the concepts of perimeter and area. It also encourages a systematic approach so that all possible shapes are found.Possible approach
You could display a square grid on your interactive whiteboard and have the pen tool ready. Make sure pairs of pupils have centimetre squared paper and pencils. Throw two dice and invite children to calculate their product. Ask them to draw a shape on their paper which has either that area or that perimeter. Suggest that they try to find as many as they can. Use the whiteboard to share their solutions.Throw the dice again and have another go. This time, once solutions have been shared, spend some time discussing ways of approaching the task, including ways of working systematically to ensure all possibilities have been found. You could make sure each child has laminated centimetre squared paper so that they can hold up their sheets. This means that everyone can see who has got the same shape and who has drawn something different. You could invite children to line up at the front of the room so that all the different shapes are displayed for a particular product. Can the class arrange them in an order? This will help them to understand what we mean by 'working systematically'.
You can then introduce the game aspect so that pairs can play against each other, perhaps with a target score of 10 at first.
Look out for children who are working systematically and those who have made connections. For example, once a shape has been found with a particular perimeter, some may notice that the same perimeter can be achieved by cutting out one or more corner squares.
Key questions
How can the dice help you draw a shape with that area?Have you got all the shapes with that area/perimeter? How do you know?
How could you 'tweak' that shape to get another with the same perimeter?
Possible extension
Invite children to change an aspect of the game by asking "what would happen if ...?". For example, "what would happen if I used a different number of dice?"; "what would happen if I added the numbers on the dice?" ...Possible support
You could suggest children play the game only focusing on area or only focusing on perimeter at first.You may also like
Geoboards
This practical challenge invites you to investigate the different squares you can make on a square geoboard or pegboard.
Tiles on a Patio
How many ways can you find of tiling the square patio, using square tiles of different sizes?
Pebbles
Place four pebbles on the sand in the form of a square. Keep adding as few pebbles as necessary to double the area. How many extra pebbles are added each time?