Build it Up

Build it Up

 

Build it Up printable sheet

 

We start with any four numbers (not zero!):



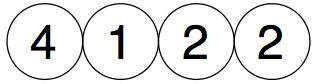
We then add them in pairs and place the total above them:



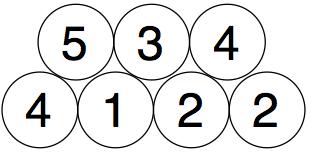
And we then add in pairs the new numbers we just got:



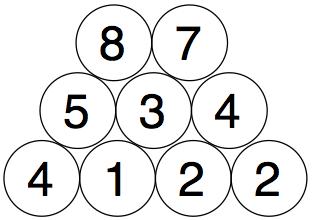
We do the same with those two numbers to get our final number:

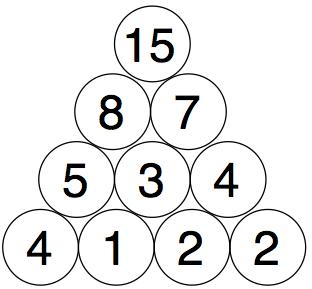
You need to find four starting numbers to place at the bottom so that the top number will be 15.

Try to find as many sets of four starting numbers as you can.

Think about good ways to do this. Maybe use a system!

What little change can you make to the rules to explore again?

What new ideas can you think of to make this different? Explore those!

You may like to take a look at the follow-on activity Build it up More.

Why do this problem?

This activity was initially developed for Wild Maths, our sister site, to encourage learners to be creative mathematicians. Mathematics is certainly a creative subject. It involves spotting patterns, making connections, finding new ways of looking at things and using what you already know in new contexts. Creative mathematicians play around with examples, draw pictures, have the courage to experiment and ask good questions. (Wild Maths is aimed at individual learners, rather than teachers, so the notes below only appear on NRICH.)

Possible approach

When the simple rules have been outlined and the example worked through some pupils may be happy recording their trials on paper. Some children might like to have little circles of paper/plastic/wood that they can write numbers on and so place them accordingly.

When a number of solutions have been found some good discussions may be had with the pupils sharing their observations as to what they notice and what does not work.

Key questions

Tell me about what's happening with the ideas you've tried.
Tell me about what's happening here (where they are at at the moment)

Possible extension

One way of extending this task is to start with more numbers at the bottom. For example, children could start with a triangle with these seven numbers at the bottom: 1, 2, 4, 8, 16, 32 and 64. These numbers can be added in the same way and pupils can see what they notice about the numbers they find at each level of the triangle. Some children might enjoy having a go at Build it Up More which is a 3D version of the challenge.

Possible support

If some pupils need help with keeping a record of what they've done, some adult support may be required.