Skip over navigation
Exploring Diagonals
We had some great solutions submitted to this problem. Well done to everyone who thought about it!
Adam from Sacred Heart School worked out the meaning of the purple number:
The purple number created, by changing the quadrilateral so it has a
different length and width, is calculated by how many squares the line
between 0,0 and the diagonally opposite corner of the quadrilateral passes
through.
e.g. if the coordinates of the opposite corner to 0,0 was 12,1 the purple
number would be 12 as it only passes through 12 squares. But the
coordinates were 2,3 the purple number would be 4.
Max and Jack from Hitchin Boys' School found a way to calculate the purple number at co-ordinates $(x,y)$:
You can calculate the purple number by adding the $x$ and $y$ values and then subtracting their highest common factor.
Several other people got this as a way to work out the purple number as well. Felix from the German American International School gave a really clear explanation of how he worked this out here.
Chenthuran from Chamblee Charter High School found some rectangles which would produce a purple number of $24$:
There are more than one set of dimensions of a rectangle for which the
purple number is $24$. Some are $24 \times1$, $24 \times 2$, $24 \times 3$, $24 \times 4$, $24 \times 6$, $24 \times 8$, $24 \times 12$, and $24 \times 24$.
Thank you everyone!
Adam from Sacred Heart School worked out the meaning of the purple number:
The purple number created, by changing the quadrilateral so it has a
different length and width, is calculated by how many squares the line
between 0,0 and the diagonally opposite corner of the quadrilateral passes
through.
e.g. if the coordinates of the opposite corner to 0,0 was 12,1 the purple
number would be 12 as it only passes through 12 squares. But the
coordinates were 2,3 the purple number would be 4.
Max and Jack from Hitchin Boys' School found a way to calculate the purple number at co-ordinates $(x,y)$:
You can calculate the purple number by adding the $x$ and $y$ values and then subtracting their highest common factor.
Several other people got this as a way to work out the purple number as well. Felix from the German American International School gave a really clear explanation of how he worked this out here.
Chenthuran from Chamblee Charter High School found some rectangles which would produce a purple number of $24$:
There are more than one set of dimensions of a rectangle for which the
purple number is $24$. Some are $24 \times1$, $24 \times 2$, $24 \times 3$, $24 \times 4$, $24 \times 6$, $24 \times 8$, $24 \times 12$, and $24 \times 24$.
Thank you everyone!
You may also like
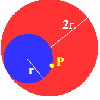
Just Rolling Round
P is a point on the circumference of a circle radius r which rolls, without slipping, inside a circle of radius 2r. What is the locus of P?
Is There a Theorem?
Draw a square. A second square of the same size slides around the first always maintaining contact and keeping the same orientation. How far does the dot travel?
