Skip over navigation
Thank you to everyone who submitted solutions to this problem. There were lots of good solutions; well done!
Ollie and Ziggy, from Priestlands School, made this observation:
The line goes: up 1 step, diagonally 1 step, across 1 step, diagonally 2 steps, and so on.
Each new diagonal line is 1 step longer than the last diagonal line.
Matt, Tom and Ollie, also from Priestlands School, were able to tell us how to work out the number of points in the previous rows.
The lengths of the diagonals can be found by adding $1+2+3+4+5+...$, ending at the length of the final diagonal.
These sums are also known as the triangle numbers.
Sunny, from Carmel Pak U Secondary School, Hong Kong, and Phil, from Our Lady of Lourdes School, Canada were able to use this to find the coordinates of 100. Here is Sunny's solution:
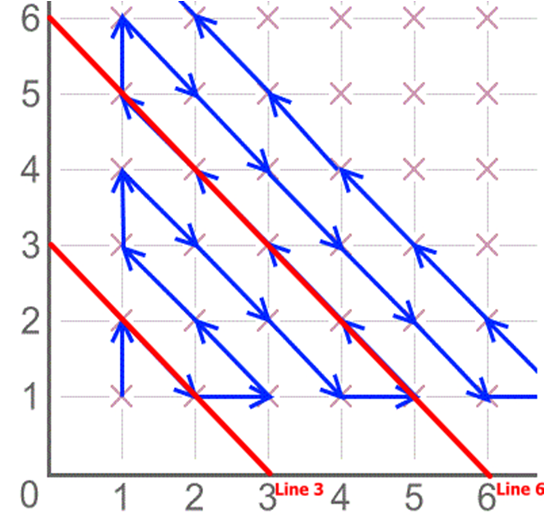
Looking at the 15th line, this has $1+2+3+4+5+6+7+8+9+10+11+12+13+14 = 105$, so we are ahead by $5$ dots.
Since line three goes down, line 4 goes up and in general the even lines go up and the odd lines go down, the line is going down.
Therefore: $105$ is at $(14,1)$.
$104$ is at $(13,2)$
$103$ is at $(12,3)$
$102$ is at $(11,4)$
$101$ is at $(10,5)$
$100$ is at $(9,6)$
Sunny then went on to describe how to find the number at $(60,40)$.
Since $60+40=100$, $(60,40)$ is on line $100$, so the final number on this diagonal is $4950$, as this is $1+2+3+4+...+98+99$.
Since $100$ is even, this line is going up, so we need to go back $59$ steps to get back to $(60,40)$.
This means the number is $4950 - 59 = 4891$.
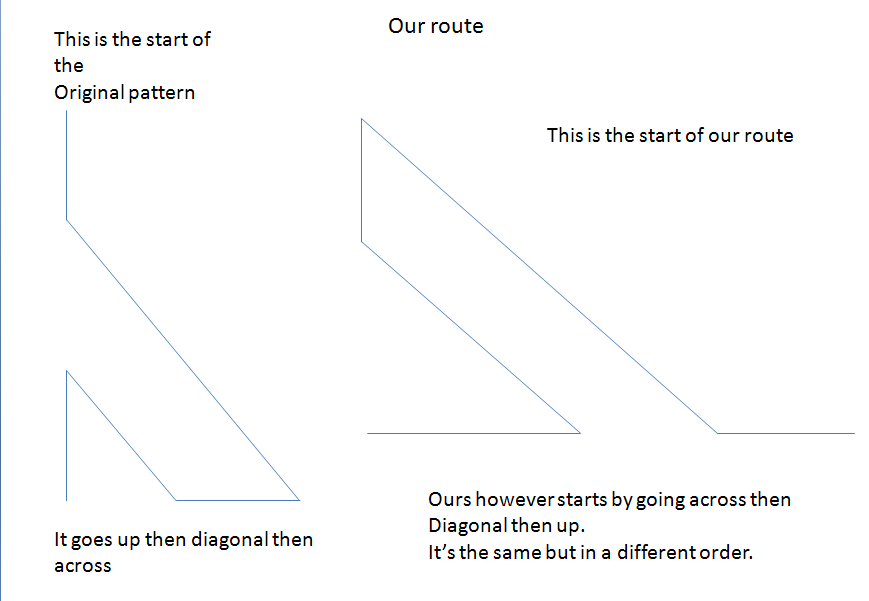
Ziggy and Ollie found an alternative route that visited all the numbers:
Sunny found a different alternative route:
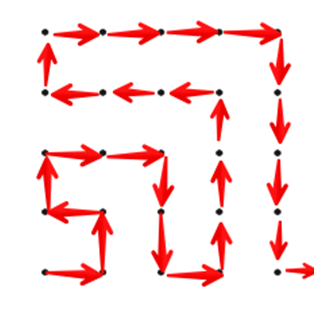
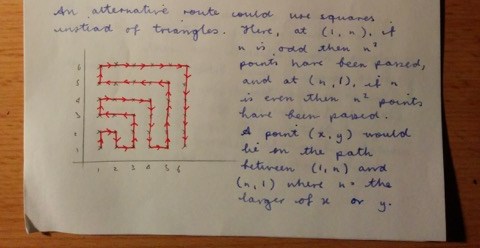
Hannah sent in this solution which explained very clearly how she was able to work out how far along the route each point was:
Hannah went on to describe the same alternative path as Sunny. She was also able to say how long it would take to reach $(60,40)$ on this path.
This reminded me of Picturing Triangle Numbers, which you might want to take a look at.
Well done and thank you to everyone who submitted solutions.
Are We Nearly There?
Thank you to everyone who submitted solutions to this problem. There were lots of good solutions; well done!
Ollie and Ziggy, from Priestlands School, made this observation:
The line goes: up 1 step, diagonally 1 step, across 1 step, diagonally 2 steps, and so on.
Each new diagonal line is 1 step longer than the last diagonal line.
Matt, Tom and Ollie, also from Priestlands School, were able to tell us how to work out the number of points in the previous rows.
The lengths of the diagonals can be found by adding $1+2+3+4+5+...$, ending at the length of the final diagonal.
These sums are also known as the triangle numbers.
Sunny, from Carmel Pak U Secondary School, Hong Kong, and Phil, from Our Lady of Lourdes School, Canada were able to use this to find the coordinates of 100. Here is Sunny's solution:
Looking at the 15th line, this has $1+2+3+4+5+6+7+8+9+10+11+12+13+14 = 105$, so we are ahead by $5$ dots.
Since line three goes down, line 4 goes up and in general the even lines go up and the odd lines go down, the line is going down.
Therefore: $105$ is at $(14,1)$.
$104$ is at $(13,2)$
$103$ is at $(12,3)$
$102$ is at $(11,4)$
$101$ is at $(10,5)$
$100$ is at $(9,6)$
Sunny then went on to describe how to find the number at $(60,40)$.
Since $60+40=100$, $(60,40)$ is on line $100$, so the final number on this diagonal is $4950$, as this is $1+2+3+4+...+98+99$.
Since $100$ is even, this line is going up, so we need to go back $59$ steps to get back to $(60,40)$.
This means the number is $4950 - 59 = 4891$.
Ziggy and Ollie found an alternative route that visited all the numbers:
Sunny found a different alternative route:
Hannah went on to describe the same alternative path as Sunny. She was also able to say how long it would take to reach $(60,40)$ on this path.
Hannah also made an excellent observation about her two paths, which she could use to connect square and triangle numbers. She used algebra to prove that this relationship would always work.
This reminded me of Picturing Triangle Numbers, which you might want to take a look at.
Well done and thank you to everyone who submitted solutions.
You may also like
Pair Sums
Five numbers added together in pairs produce: 0, 2, 4, 4, 6, 8, 9, 11, 13, 15 What are the five numbers?
Summing Consecutive Numbers
15 = 7 + 8 and 10 = 1 + 2 + 3 + 4. Can you say which numbers can be expressed as the sum of two or more consecutive integers?
Big Powers
Three people chose this as a favourite problem. It is the sort of problem that needs thinking time - but once the connection is made it gives access to many similar ideas.