Reasoned Rounding
Reasoned Rounding
Reasoned Rounding printable sheet
This is a rounding game for two players.
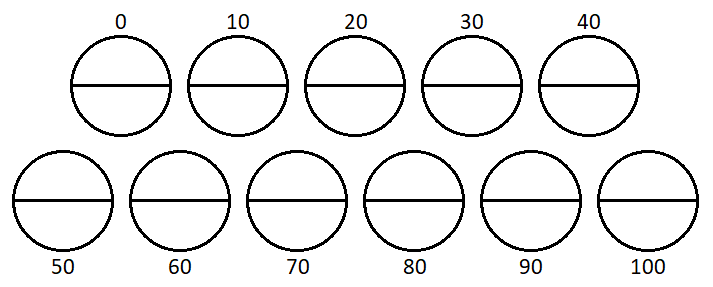
You will need a recording sheet shared between the two players. One sheet is enough for three games.
The first player rolls a 0-9 dice twice and chooses which two-digit number they would like to make from the numbers rolled.
They then round this number to the nearest 10, find the matching circle on the recording sheet and write their two digit number in one of the spaces in that circle.
The second player rolls the dice twice to take their turn in a similar way.
A circle is complete when it has two numbers in it and this scores a point for the person who wrote the second number in. (Even if the first number was written in by the other player.)
The game is over when all the circles are full and then the points are counted up to find the winner.
Why do this problem?
The game offers a competitive context which provides pupils with lots of practice in rounding numbers and helps develop their reasoning by encouraging them to talk about their strategies for winning points whilst playing.
Possible approach
Play as a class first by projecting the recording sheet onto the board and asking pupils to roll dice, suggest what numbers could be made and explain to the class where they would want to put them and why.
Key questions
What two-digit numbers can you make from the digits you rolled?
Where might be a good place to put your number?
What numbers are you hoping might come up on your next turn?
Can you explain why you chose that circle?
Possible extension
Some other versions of the same game are available here:
Reasoned Rounding to the nearest hundred recording sheet
This time the players roll the dice three times each per turn and can be encouraged to record the different 3-digit numbers possible before making strategic decisions as to where they could best place their chosen number.
Reasoned Rounding to the nearest whole number recording sheet
Players roll the dice twice and then place one number on each side of a decimal point. They round their chosen number to the nearest whole number and then place it in the appropriate circle as before.
Reasoned Rounding to the nearest tenth recording sheet
Players still roll the dice twice, but then decide in which order to place them after a decimal point. Having created a number which has two decimal places, they must then round it to the nearest tenth and place it in the appropriate space on the recording sheet.
What other variations can pupils come up with for themselves?
What if they were to use different dice? What recording sheets would be needed now?
Possible support
Ask pupils to play in groups of four, one pair against another, in order to support their discussion of options whilst carrying out the rounding.
You may also like
Chocolate
There are three tables in a room with blocks of chocolate on each. Where would be the best place for each child in the class to sit if they came in one at a time?
Four Triangles Puzzle
Cut four triangles from a square as shown in the picture. How many different shapes can you make by fitting the four triangles back together?
Cut it Out
Can you dissect an equilateral triangle into 6 smaller ones? What number of smaller equilateral triangles is it NOT possible to dissect a larger equilateral triangle into?