Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Beach Huts



- Problem
- Student Solutions
- Teachers' Resources
Why do this problem?
This problem invites students to look at a few examples, notice and explain patterns, and then generalise. Many questions about sequences just look at a single variable. As each beach hut contains several linked numbers, there are several different sequences to spot and explain.
Possible approach
Display the first image of beach huts.
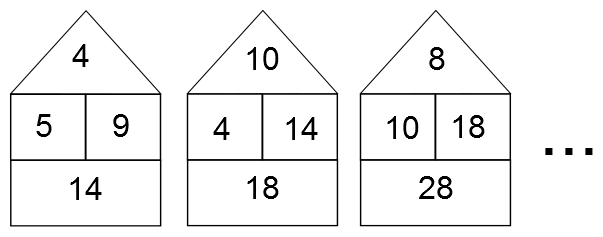
"Here is a sequence of beach huts. Take a moment to look at them and see what you notice."
"Now turn to your partner and discuss what you noticed. Did you see the same things?"
"With your partner, see if you can agree what the next beach hut in the sequence might look like."
Once students have had a chance to draw the next beach hut, take some time to discuss everything they noticed, and agree as a class how the numbers in a hut are related and how each hut is related to the previous one.
Here are some questions that you may wish to invite students to explore:
- If you know any pair of numbers from a beach hut, can you work out the other two numbers?
- Can you find a sequence of beach huts where two adjacent huts have the same roof number?
- If you know the numbers in a hut, how can you work out the numbers of the fourth hut to the right of it? Or the 10th? Or the 100th...?
- If you know the numbers in a hut, how can you work out the numbers of the sixth hut to the left of it? Or the 12th? Or the 100th...?
- If you know the numbers in a hut, how can you work out the numbers of the seventh hut to the right of it? Or the fifth hut to the left of it? Or the 99th in either direction...?
To work on these questions, students could generate sequences of beach huts of their own and look for rules linking the numbers between huts. You may wish to introduce an algebraic representation where the middle two numbers in the hut are $a$ and $b$, and invite students to work out other terms in the sequences algebraically.
At the end of the session, bring the students together and set them a challenge: "Here is a beach hut. Without drawing all the huts in between, quickly draw for me the 5th and 8th hut to the right." If you have mini whiteboards the students could draw their huts and then hold them up to see if everyone agrees. Finally, invite students to compare how they worked out the numbers.
Possible support
Encourage students to draw the next few beach huts in the original sequence and look for as many different patterns as they can, before trying to explain those patterns.
Challenge them to go both to the right and to the left.
Possible extension
Coordinate Patterns challenges students to describe sequences on a coordinate grid.
You may also like
Summing Consecutive Numbers
15 = 7 + 8 and 10 = 1 + 2 + 3 + 4. Can you say which numbers can be expressed as the sum of two or more consecutive integers?
Always the Same
Arrange the numbers 1 to 16 into a 4 by 4 array. Choose a number. Cross out the numbers on the same row and column. Repeat this process. Add up you four numbers. Why do they always add up to 34?
Fibs
The well known Fibonacci sequence is 1 ,1, 2, 3, 5, 8, 13, 21.... How many Fibonacci sequences can you find containing the number 196 as one of the terms?

