Overlaps

Overlaps printable sheet

Seven Regions

Place the digits $1$ to $7$, one in each region, so that the circles all have the same total.

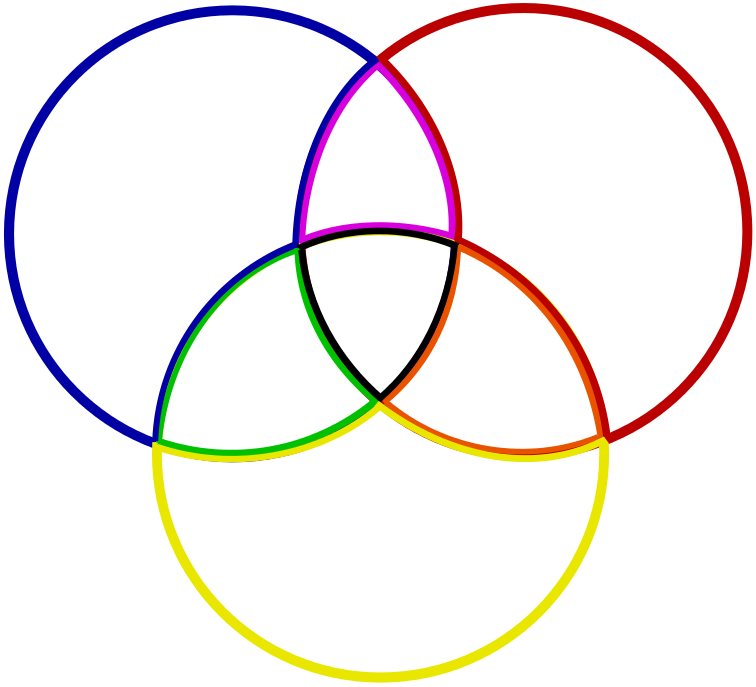
Can you also show that:

• you cannot have a circle total of $16$ with $4$ in the centre?
• you cannot have circle totals greater than $19$ or less than $13$?
• you cannot have anything other than $1$ in the centre for a circle total of $13$?

Five Rings

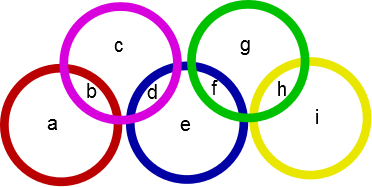
These five rings create nine regions, labelled $a$ to $i$ above. Using each of the digits $1$ to $9$ exactly once, can you place one number in each region so that the sum of the numbers within each ring is the same?

Can you find more than one solution?

Show that for any solution the sum of the numbers in the overlaps ($b$, $d$, $f$ and $h$) must be a multiple of $5$.

Using this, can you find a lower and an upper bound for the possible ring totals?

Is there a solution for every ring total between the lower and upper bound? 
If not, can you prove that no such solution exists?

If you enjoyed this problem, you may also like to take a look at Magic Letters.

With thanks to Don Steward, whose ideas formed the basis of this problem.