Same Answer

Same Answer printable sheet

Aisha has been practising arithmetic with fractions.

She worked out $4\frac{1}{2} - 3$ but then she realised that she had misread the question, and the teacher had actually asked her to work out $4\frac{1}{2} \div 3$
When she worked out the division, she was surprised to find she got the same answer to both calculations!

Aisha decided to look for other calculations where replacing the division sign by a subtraction sign does not alter the result of the calculation.

Here are some of the examples she tried:

$3\frac12 - 2$ and $3\frac12 \div 2$

$5\frac12 - 4$ and $5\frac12 \div 4$

$5\frac13 - 4$ and $5\frac13 \div 4$

$6\frac17 - 5$ and $6\frac17 \div 5$

$7\frac15 - 6$ and $7\frac15 \div 6$

Which of Aisha's examples give the same answer for both calculations?
Can you spot any patterns?

Click below to see two different observations about the examples where the answer is the same.

"I noticed that in the examples that worked, the denominator in the fraction was one less than the number being subtracted."

"I drew a diagram to help me understand:

 
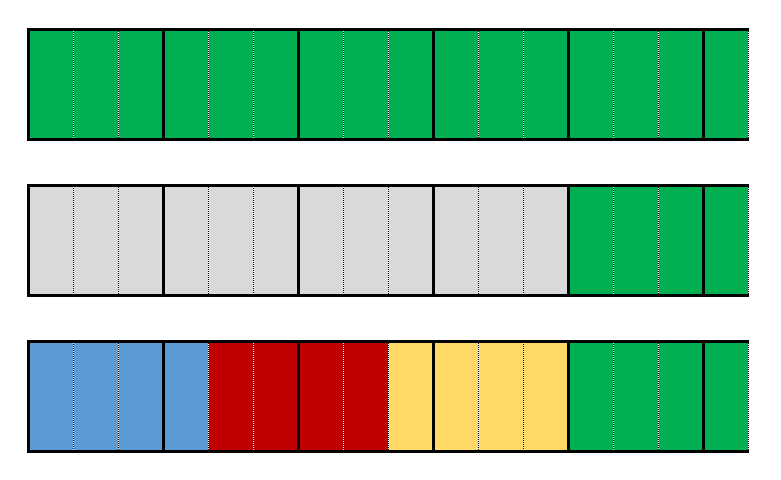
The top shows $5\frac13$.
The second row shows $5\frac13-4$
The third row shows $5\frac13\div4$."
 

Can you find a general rule?


Extension:

Can you justify this rule algebraically? 

What happens if you replace the subtraction sign with an addition sign?



With thanks to Don Steward, whose ideas formed the basis of this problem.