Same Answer

Why do this problem?

Even if they have met calculation with fractions before, students often need more practice. It is important to address this without it feeling like an exact repetition of what they have done many times before. This problem lets you spot misconceptions your students have about subtraction and division of fractions, while giving students an opportunity to practice the procedures in an intriguing context - students' curiosity will be raised by the strange patterns in the calculations, and we hope they will yearn to explain what is happening.

Possible approach

Share the following problem with the class:

Aisha has been practising arithmetic with fractions.

She worked out $4\frac{1}{2} - 3$ but then she realised that she had misread the question, and the teacher had actually asked her to work out $4\frac{1}{2} \div 3$
When she worked out the division, she was surprised to find she got the same answer to both calculations!

Firstly you might like to ask the class to verify the claim. Use this time to circulate and look for students who may need a reminder of how to calculate with fractions. You may also find students using different strategies and it would be worth sharing some of these with the class. 

Once you have agreement and some strategies to use you could ask your students to try out some more examples.

Which of the following pairs of statements are equal?

$3\frac12 - 2$ and $3\frac12 \div 2$

$5\frac12 - 4$ and $5\frac12 \div 4$

$5\frac13 - 4$ and $5\frac13 \div 4$

$6\frac17 - 5$ and $6\frac17 \div 5$

$7\frac15 - 6$ and $7\frac15 \div 6$

Give students some time to calculate each example and check for themselves.

Once everyone has figured out which ones are equal, write them on the board in a list. 
Students may make the following observations:

• The denominator of the fraction is 1 less than the number being subtracted.
• The whole number part is 1 more than the number being subtracted.

Invite students to try some more examples based on any observations they have made, and to see if they can explain why they work. While students are working, take a look at what they're doing and invite students working on any interesting representations to share them with the class.

You might like to share the representation from the problem as a prompt.


 
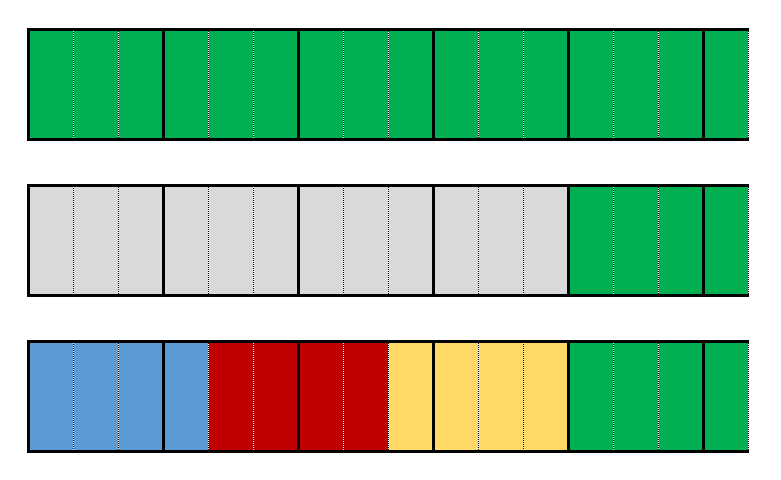
The top shows $5\frac13$.
The second row shows $5\frac13-4$
The third row shows $5\frac13\div4$.

Possible support

For a similar idea with adding and multiplying fractions students could work on Sum Equals Product.

Possible extension

Students who are comfortable using algebra could be asked to represent their results algebraically.

Fair Shares is another example of a fractions problem that leads to algebra and some generalisation.