Maxi Pyramid

Five integers (whole numbers) are placed on the bottom row of this pyramid.  They must satisfy the following conditions:

• No zeros or negative numbers are allowed
• The five numbers on the bottom row must add up to $20$
   

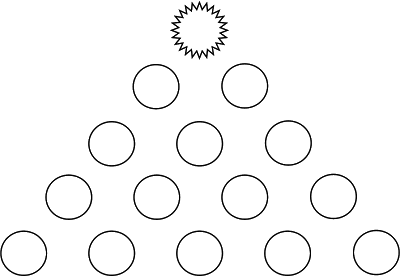
Each number in the upper rows of the pyramid is formed by combining the two numbers below it, according to the following rules:

• If the two numbers below are even, you add them to get the one above
• If the two numbers below are odd, you take the smaller from the larger to get the one above
• If one number is odd and one is even, you multiply the two numbers to get the one above

Try starting with $4, 6, 1, 7, 2$ on the bottom row. What do you get at the top?
 

What is the largest top number you can obtain?

Extension:

What is the largest top number you can obtain if zeroes are allowed?
What is the largest top number you can obtain if negative numbers are allowed?


With thanks to Don Steward, whose ideas formed the basis of this problem.