Maxi Pyramid

We received lots of large top numbers. Rachel from Holy Child Killiney in Ireland got 122:

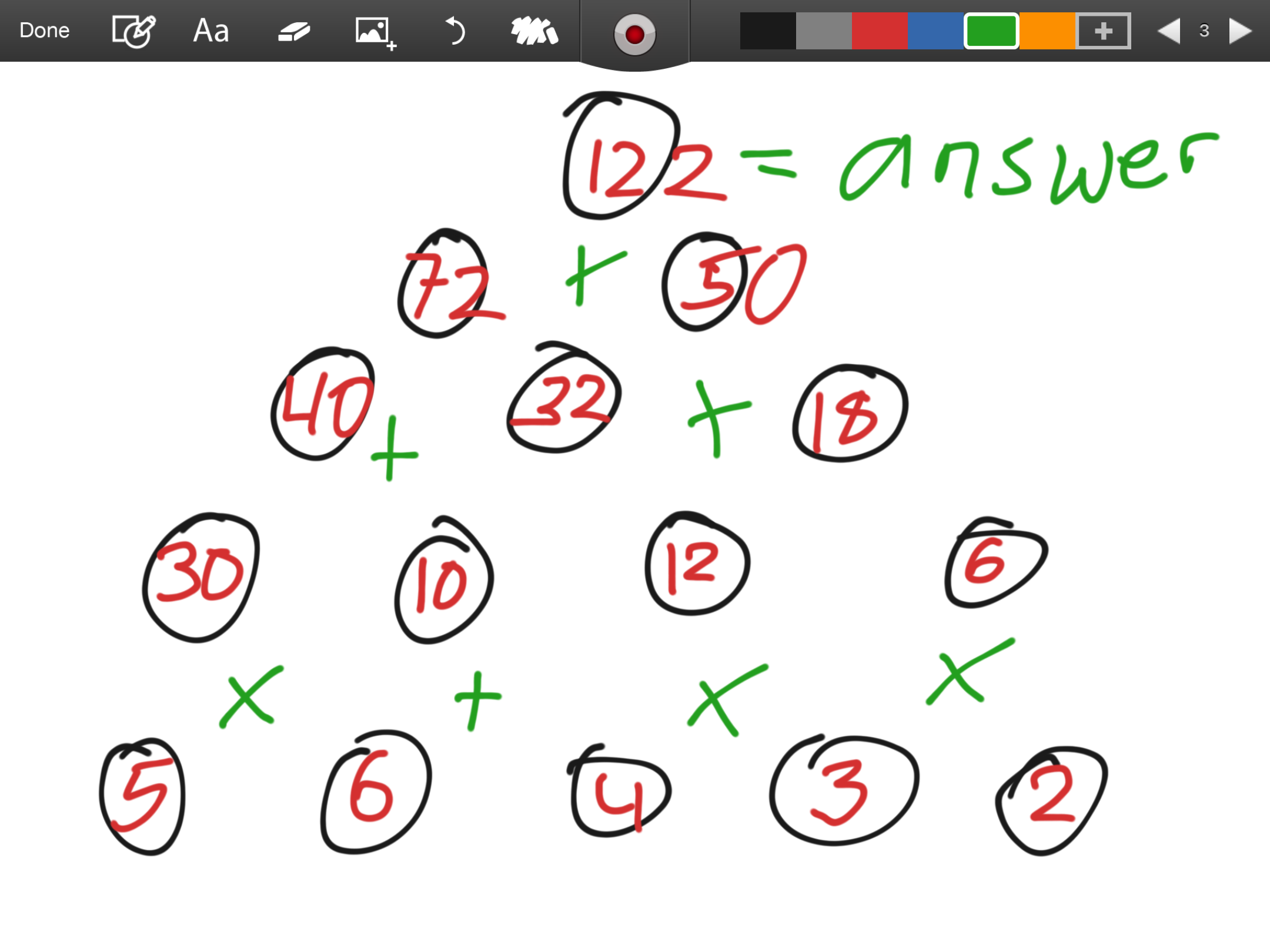
 Aila, Lathika, Addisyn and Tamsyn from Frederick Irwin Anglican School in Australia sent in this pyramid with some of their reasoning:

Toby from Pierrepont Gamston Primary School in England wrote:

The most I got was 128 as the top number. On the bottom, it was 4, 3, 4, 5, 4. I did this because I wanted the largest numbers I could shared out and I want to do as much multiplication as possible and as explained, an odd and an even get multiplied.

Alonso and Santiago from Colegio Roosevelt in Peru sent in several Maxi pyramids:

Roisin from Holy Child Killiney sent in this pyramid:

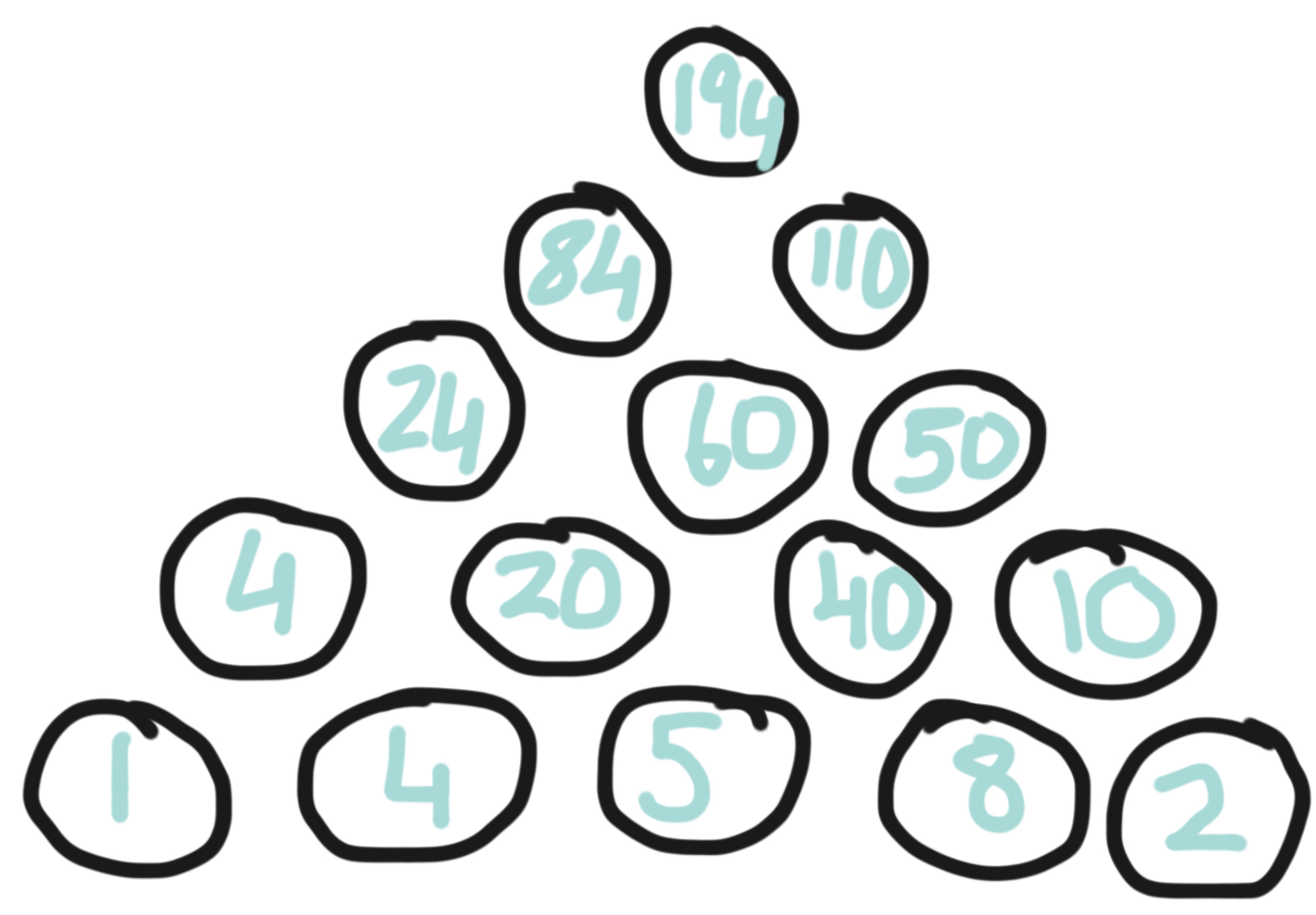
Amélie from St Nicholas CE Primary in England sent in this pyramid:

           200
        116  84
     56   60   24
  14   42   18   6
 2    7    6    3    2

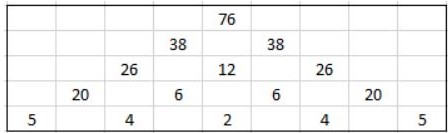
Olly from Warden Park in England:

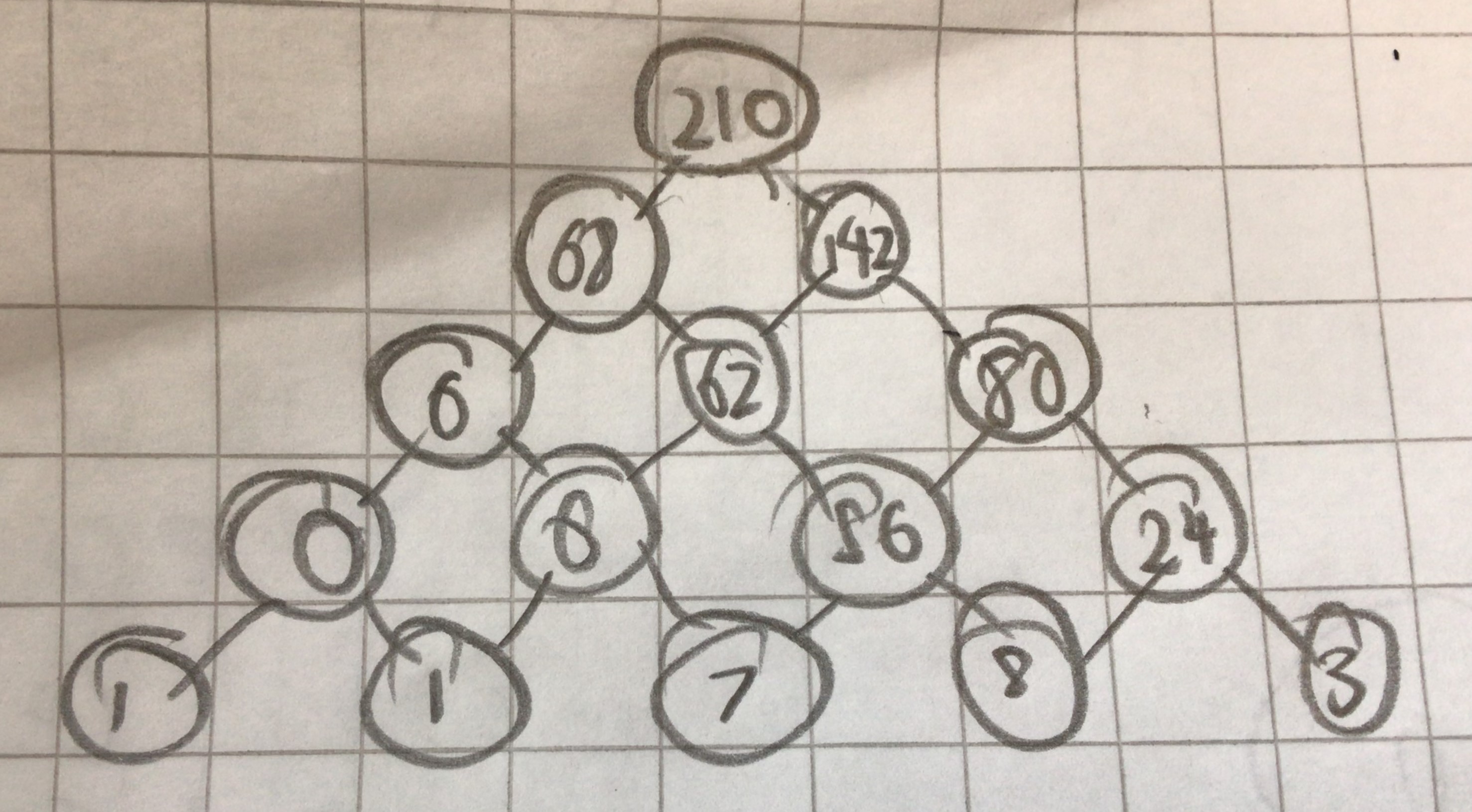
Per André from Hakadal Ungdomsskole in Norway sent in this clear explanation and pyramid:

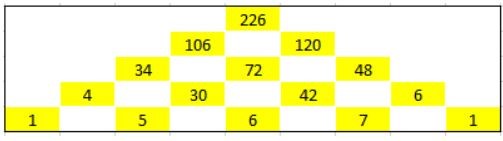
To achieve the highest number on top of the pyramid, according to the given instructions, I had to do the following:

After some time with testing, I decided that the best approach would be to place a high even number (6) in the middle. And then I put a high odd number (5 and 7) as possible on each side, so that I could multiply them with the one on the middle. And then I put 1 on each side, so that it sums up to 20. If I had used a bigger number on each side, the numbers in the middle would have been lower. So the most important thing to solve this, is to put the biggest numbers in the middle.

The advantage by putting the biggest numbers (5, 6, 7) in the middle, is that we also get big numbers (30, 42) in the middle on line 2. If we placed the numbers like this: 

We can see that the biggest numbers on line 2 is placed on each side, and not in the middle. This is a disadvantage, because the middle number on line 3 is made up from adding two small numbers.

I.A, Mignione, Saskia.B from Frederick Irwin School managed to get an even larger number at the top of their pyramid:

Ramya, Reef and Caleb from Frederick Irwin School had another idea:

We found out that if you make an odd number on a high level of the pyramid then there will be an even number most likely next to it and they will multiply together to make a huge number.

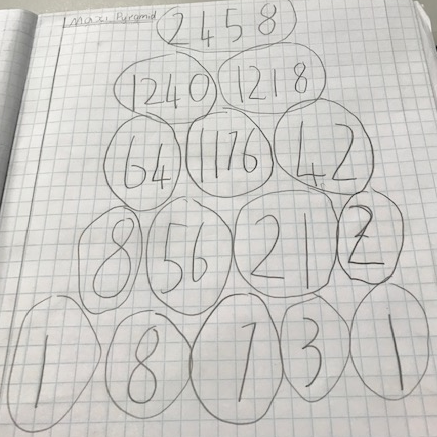
This was a very good idea, but can you see where they broke one of the rules?

Is it possible to make an odd number on a high level of the pyramid?

Ci Hui Minh Ngoc from Kelvin Grove State College (Brisbane) in Australia thought harder about odd and even numbers:

This strategy helped Ci Hui Minh Ngoc get 222 at the top of the pyramid: