Growing Surprises

Age 11 to 14

Challenge Level Yellow star

Thank you to everybody who submitted solutions for this problem. Here's how some of you thought about the problem:

Tor, from Harbinger School, UK, and Edi, Joseph, Vladimir and Alastair, from The British International School of Shanghai Puxi, China, had a similar approach to the first part of the problem:

I first found the total number of squares in each pattern, and then computed the differences between them. So, the totals are: 8, 16, 24, 32, ... Therefore, the difference between any 2 neighbours is 8, so the $n^\text{th}$ pattern has $8n$ squares.

Then I can easily work out the number of squares in the $ 20^\text{th}$ pattern (there are $8$ x $20 = 160$ squares) or in the $50^\text{th}$ pattern ($8$ x $50 = 400$ squares).

Abby and Rebecca, from the British International School, Shanghai, Puxi campus, and Rosie Coward, from Wycombe High School, England, worked out the formula for the second pattern:

Taking the next sequence, we realised that these were the same shapes, but filled in, rather than hollow. We counted each number of squares from the first patterns, and worked out the differences between each neighbour. Then we did that again, with the new sequence:

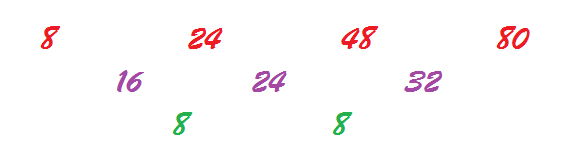
So the second difference is 8. Since to find the multiplier (coefficient) of the squared number, you must divide the second difference by two, we found the first term, $4n^2$. Comparing this new sequence $(4, 16, 36, 64)$ to our original one gives a difference of $4n$. Therefore, the number of squares in the $n^\text{th}$ pattern is $4n^2 + 4n$.

From there we found the next 3 terms (120,168, 224), and then found the 20th term (1680)
and the 50th (10200).

Tim, from Gosforth Academy, UK, used a geometric approach to the problem:

Each shape consists of two $2n-1$ sides (the left and right ones, in green) and two $2n+1$ sides (the top and bottom ones, in pink). The diagram shows the $n=6$ case:

Therefore, the total number of squares in the $n^\text{th}$ pattern is $2(2n+1) + 2(2n-1) = 8n$.

Interestingly, if we fit the pieces into each other, we get the solid shapes shown in the second sequence:

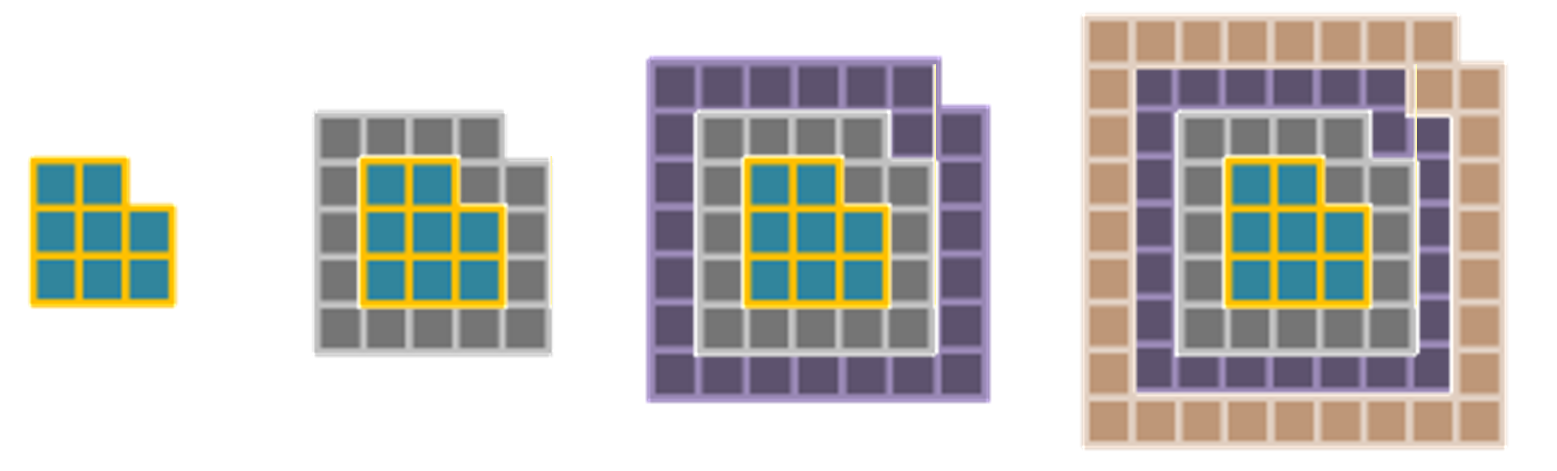
If we say that the areas in the first sequence are $A_1, A_2, A_3, A_4, ...$ and the areas in the second sequence are $B_1, B_2, B_3, B_4, ...$ we then have that $B_4 = A_1 + A_2 + A_3 + A_4$ (by looking at the fourth picture). Generally, $B_n = A_1 + A_2 + ... + A_n$.

From before, $A_n = 8n$ for each $n$. Hence, $B_n = 8 (1 + 2 + ... + n)$.

But $1+2 +...+n$ is the $n^\text{th}$ triangular number. So, $B_n = 8$ x the $n^\text{th}$ triangular number.

This makes sense geometrically:

In the last figure, the $4^\text{th}$ triangular number appears $8$ times. Notice that the gap in the middle corresponds to the missing dot in the top right figure of the original pattern.

Using the formula for the $n^\text{th}$ triangular number we get: $B_n = 8 n (n+1)/2$, so $B_n = 4n(n+1) = 4n^2 + 4n$.

Michael and Lera, from Harbinger Primary, UK, expressed it in a slightly different way.

In the second sequence, each pattern is obtained from the previous one in the sequence, plus a contour from the first sequence:

Therefore, the area of a pattern is $8n + $ the area of the previous pattern.

Nia from School No. 97, Bucharest, Romania, created the next two patterns in each of the first two sequences, and gave a slightly different gometric interpretation:

The next two patterns (the fifth and sixth) in the first and second sequences are:

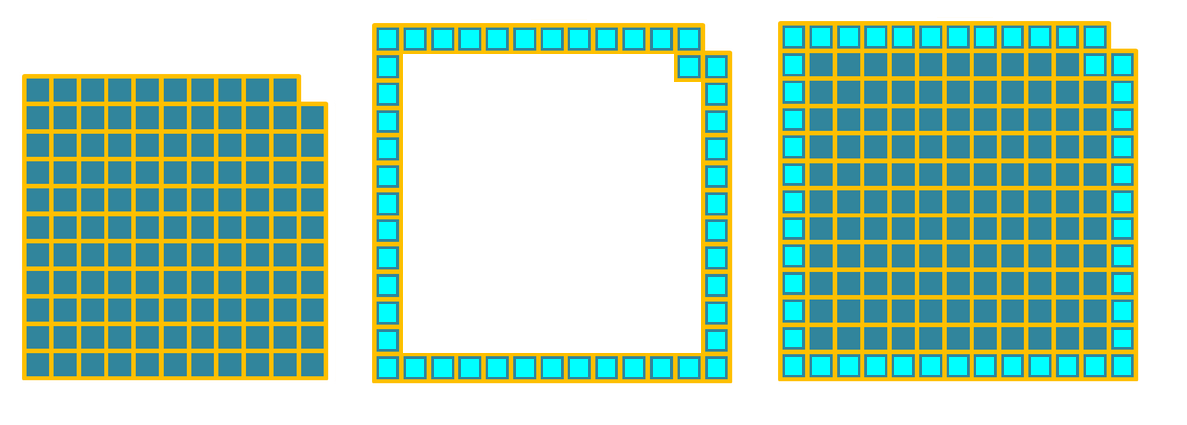
The second pattern could be described as a full $2n+1$ by $2n+1$ square, with the top right $1$ by $1$ square missing. Therefore, the number of squares is $(2n+1)\times (2n+1) -1$.

The first pattern, consists of the contour of each of these squares with the top right corner moved down diagonally. If we firstly move the top right square such that we get the contour of a $2n+1$ by $2n+1$ square, we get:

Now the number of squares are easy to count: there are four groups of $2n$ squares, so there are $8n$ squares.

Alternatively, each is the contour of an $2n+1$ by $2n+1$ square so is a $2n+1$ by $2n+1$ square with the centre (a $2n-1$ by $2n-1$ square) missing. So the area is $(2n+1)^2 - (2n-1)^2 = 4n^2 +4n + 1 - 4n^2 + 4n -1 = 8n$, the same result as before.

Ryan, from The British International School, Shanghai Puxi, China, found a relationship between the first and the second pattern:

The areas in the first sequence are $8, 16, 24, 32, ...$, while the ones in the second pattern are $8, 24, 48, 80, ...$. Now, if we divide the numbers from the second sequence by the ones in the first we get $1, 1.5, 2, 2.5, ...$. Hence, the areas in the second sequence are obtained from the ones from the first sequence by multiplying them by $0.5n + 0.5$.

This is consistent with the algebra: $4n^2 +4n = 8n (0.5n+0.5)$.

Abby and Rebecca, also from The British International School, Shanghai, Puxi campus, China, found a different relationship:

The first few terms of the first sequence are 8, 16, 24, 32, 40, 48, 56, 64, 72, 80”¦
The first few terms of the second sequence are 8, 24, 48, 80, 120...

We realised that the first numbers are the same in both the first and the second sequence.
The second number from the second sequence is the same as the third number in the first sequence.
The third number in the second sequence is the same as the sixth from the first.
And so on...
The second sequence is obtained from the first by skipping one number then two, then three...

Also, the difference between the two sequences is $4n(n-1)$.

Angela, Jessica, Brian,Frank, Abby and Rebecca, from The British International School, Shanghai, Puxi, China, have identified the number of squares in the next pair of patterns:

As we looked at the next two, we found that the same pattern occurred: the
first (linear) sequence was simply the outside 'layer' of the other (quadratic) sequence.

By counting squares, we get that the first sequence is $8, 14, 20, 26, ...$. The difference between two consecutive terms is $6$, so the $n^\text{th}$ pattern has $6n+2$ squares.

For the last sequence, we do repeated differences between consecutive terms again:

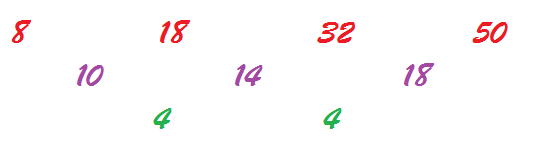
We divide $4$ by $2$ to get the coefficient of $n^2$: so we have $2n^2$. Then we subtract $2n^2$ from the original sequence for each term and we get $6, 10, 14, 18, ...$. The difference between two consecutive term is $4$, so $n$ has a coefficient of $4$. Therefore, the $n^\text{th}$ pattern of the sequence has $2n^2 + 4n + 2$ squares.

As we looked at them, we realized the reason why one was linear while the other one was quadratic. The first one was counting squares on the contour, which is simply finding the perimeter. The second one was finding the area of an almost full square, so it should have an $n^2$ term. In other words, the perimeter has only one dimension, while areas have two dimensions.

Nia from School No. 97, Bucharest, Romania, approached this part of the problem geometrically:

By moving the yellow squares from the picture below diagonally up, we can see that the first pattern is obtained from the contour of an $2+n$ by $2n+1$ rectangle. The diagram shows the $n=4$ case.

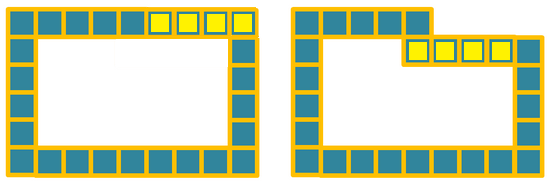
So the number of squares in the pattern is the same as in the contour of an $n+2$ by $2n+1$ rectangle, and hence, we can count the squares:

We have $2$ columns of $n+1$ squares (blue and green), and $2$ rows of $2n$ squares (pink and purple), so a total of $ 6n+2$ squares.
Alternatively, from the area of an $n+2$ by $2n+1$ rectangle, which is $(n+2) \times (2n+1)$, subtract the area of a $n$ by $2n-1$ rectangle, which is $n(2n-1)$. Therefore, the contour has $(n+2) \times (2n+1) - n(2n-1) = 6n +2$ squares for each $n$.

Yet another way of doing it was to compare this pattern with the one in the first sequence. We can construct one from another as shown in the figure below, again demonstrating the $n=4$ case:

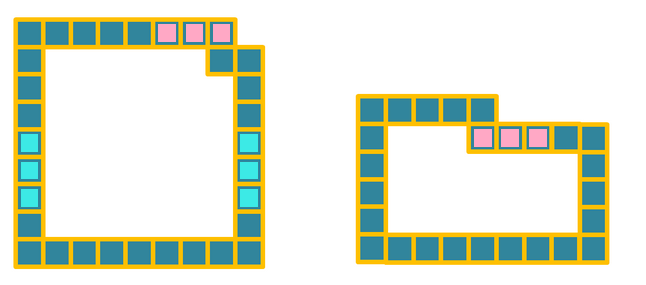
If we erase the $n-1$ blue squares on each vertical side, and move the $n-1$ pink ones down diagonally, then we get the second pattern. So the numbers of squares in the second pattern is with $2\times(n-1)$ squares less than the first one. Since the first sequence had $8n$ squares in the $n^\text{th}$ pattern, then the formula for the third one is $8n - 2(n-1) = 6n+2$, as before.

The last pattern is made from a $n+1$ by $2n+1$ rectangle (in blue) with a $1$ by $n+1$ (in red) rectangle on top. So in total, it has $(n+1)\times (2n+1) + 1\times (n+1) = 2(n+1)^2$.

Emma, Inés and Eline from King´s College, Alicante, Spain, approached the last part of the problem slightly differently:

We divided the pattern into two rectangles: The area of the first one (in red) would be $(n+1)(n+2)$, while the area of the second one (in blue) would be $n(n+1)$. The diagram shows the case where $n=4$.

Hence, the total number of squares is $n(n+1) + (n+1) (n+2) = (n+1)(2n+2) = 2(n+1)^2$.

Emily Powell, from Hymers College, England, and Vladimir and Joseph, from The British International School, Shanghai Puxi Campus, completed the rectangle instead of breaking it up:

In the second sequence we know that the number of squares missing is always equal to n. So we can add an $n$ by $1$ rectangle to our pattern (in red below) so that we get a complete $(n+2)$ by $2n+1$ rectangle. The diagram shows the case where $n=4$.

Therefore, the area will be $(n+2)(2n+1) - n = 2(n+1)^2$.

Sameer and Will, from Hymers College, England, noticed something different:

We know that the contour has $6n + 2$ squares. Then we can break the inside into two halves, as below:

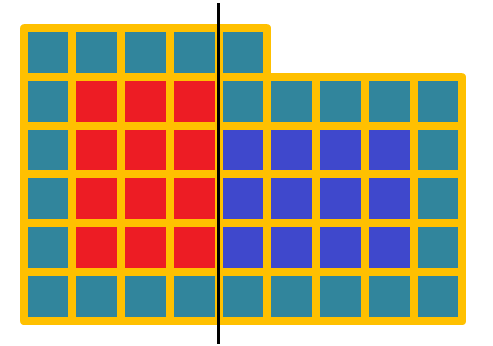
The two resulting rectangles (one in red, one in blue) have the same area: each has an area of $n(n-1)$. In the figure, $n=4$ and each rectangle has $4 \times 3 = 12$ squares.

Hence, the area of the interior part is $2n(n-1)$. We then add the area of the contour, to get the area of the whole pattern: $2n(n-1) + 6n+2 = 2n^2 +4n +2 = 2(n+1)^2$.

Well done to you all for sending such a variety of solutions!

Number and algebra

Geometry and measure

Probability and statistics

Working mathematically

Advanced mathematics

For younger learners

Growing Surprises

You may also like

Days and Dates

Summing Consecutive Numbers

Paving Paths