Growing Surprises

Growing Surprises printable worksheet
 

Take a look at the pattern below:
 

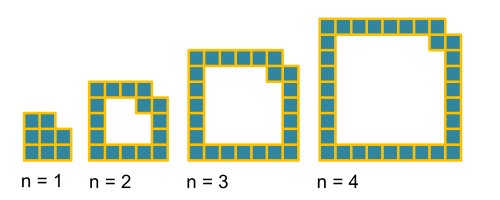
Can you describe the next few patterns in the sequence?

Can you work out how many squares there are in each pattern?

Is there a quick way to work out the number of squares in the 20th pattern? Or the 50th pattern? Or...


Here's another pattern made from squares:
 
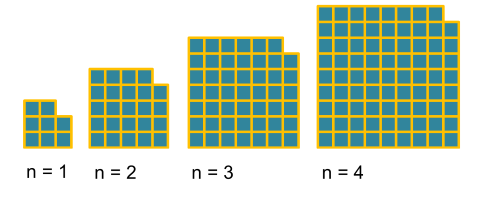
Can you describe the next few patterns in the sequence?

Can you work out how many squares there are in each pattern?

Is there a quick way to work out the number of squares in the 20th pattern? Or the 50th pattern? Or...


Can you describe any relationships between the two patterns?


Here are two similar linked patterns:


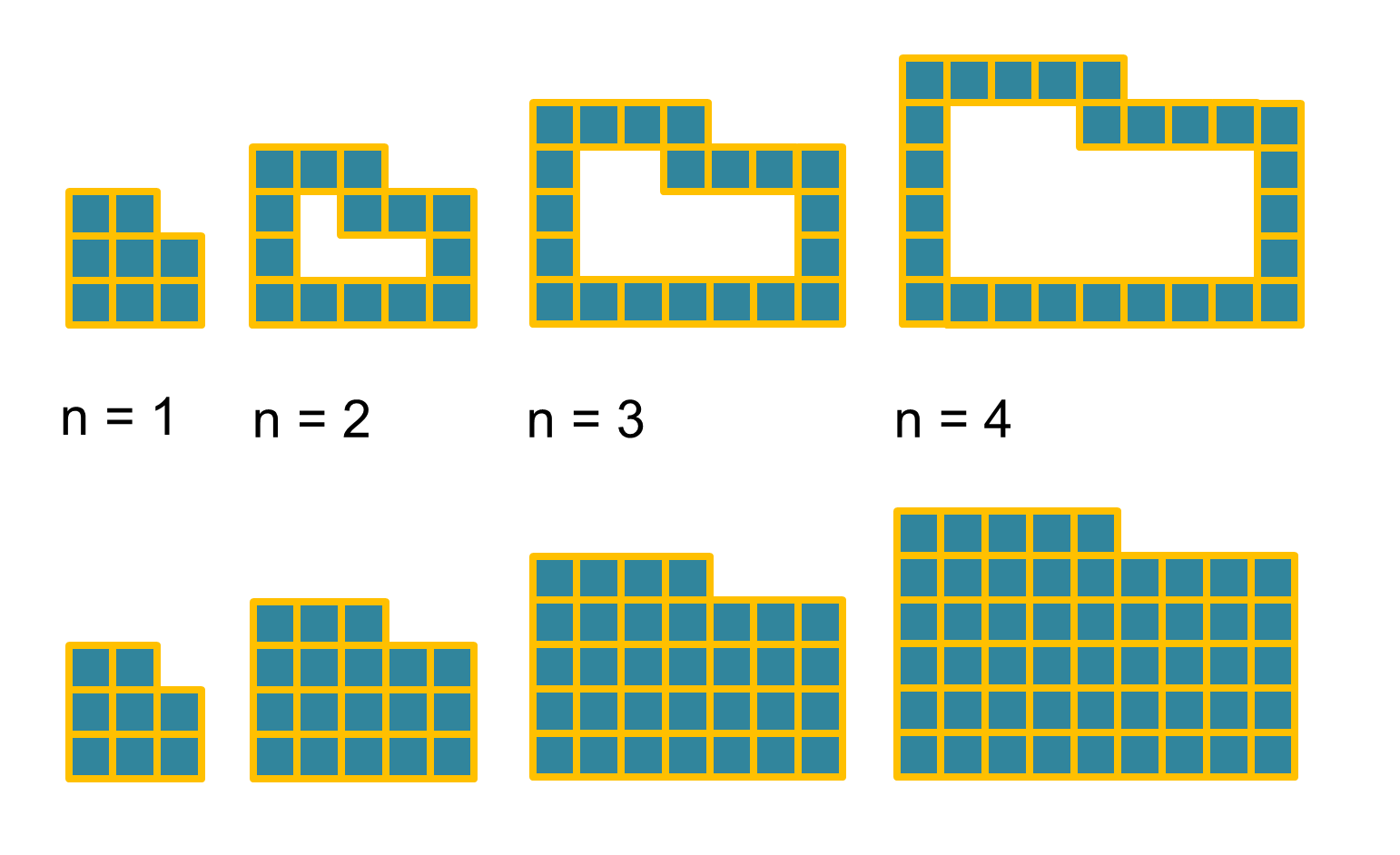
Can you find a quick way to work out how many squares there are in these patterns?
Can you describe any relationships between these two patterns?


You may wish to look at some similar problems, Seven Squares, Attractive Tablecloths and Steel Cables.



With thanks to Don Steward, whose ideas formed the basis of this problem.