Or search by topic
Number and algebra
Geometry and measure
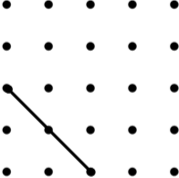
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Completing Quadrilaterals



Completing Quadrilaterals printable sheet
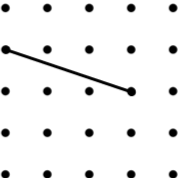
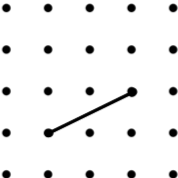
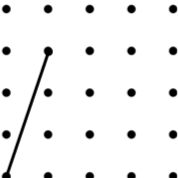
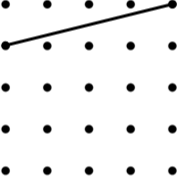
Each line is one side of the named quadrilateral. Can you draw the other three sides in the 4 by 4 dotty grids?
If there is more than one possibility, try to find the quadrilateral with the largest area (given in brackets).
An * indicates that there is a “special” quadrilateral with a larger area than the one
given in the brackets. For example, the largest parallelogram might be a square or a rectangle. Take a look at the Getting Started page if you want to find out more about special cases.
| 1. Rectangle (6) |
2. Square (8) |
3. Rectangle (4) |
 |
 |
 |
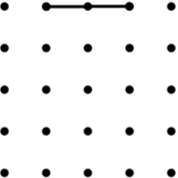
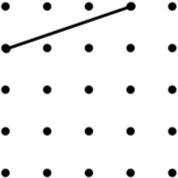
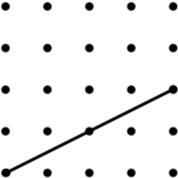
4. Isosceles Trapezium (12) |
5. Parallelogram (9*) |
6. Kite (8) |
 |
 |
 |
7. Parallelogram (6) |
8. Square (5) |
9. Kite (12) |
 |
 |
 |
10. Rhombus (4*) |
11. Parallelogram (3*) |
12. Kite (6) |
 |
 |
 |
13. Arrowhead (6) (Concave Kite) |
14. Kite (8) | 15. Rhombus (8) |
 |
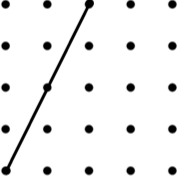 |
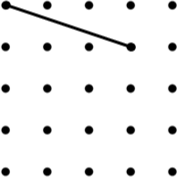 |
16. Rhombus (3) |
|
18. Trapezium (9) |
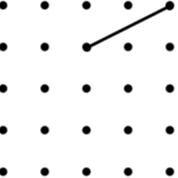 |
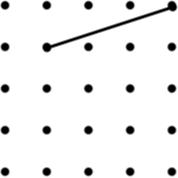 |
 |
19. Parallelogram (8) |
20. Isosceles Trapezium (8) |
21. Kite (3) |
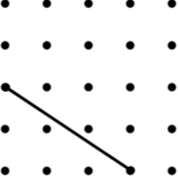 |
 |
 |
22. Arrowhead (4) (Concave Kite) |
23. Kite (9) | 24. Trapezium (9) |
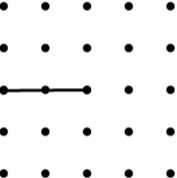 |
 |
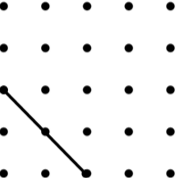 |
With thanks to Don Steward, whose ideas formed the basis of this problem.
You may also like
Linkage
Four rods, two of length a and two of length b, are linked to form a kite. The linkage is moveable so that the angles change. What is the maximum area of the kite?
Making Rectangles, Making Squares
How many differently shaped rectangles can you build using these equilateral and isosceles triangles? Can you make a square?
The Cyclic Quadrilateral
This gives a short summary of the properties and theorems of cyclic quadrilaterals and links to some practical examples to be found elsewhere on the site.

