Completing Quadrilaterals

Why do this problem?

This problem is an engaging consolidation activity - it challenges students to apply their knowledge of the properties of quadrilaterals while trying to maximise their areas on a small dotty grid.
 

Possible approach

The following printable worksheet may be useful: Completing Quadrilaterals.

You may like to play a couple of rounds of Guess my Quad with your class at the start of the lesson to clarify the properties of different quadrilaterals. 

This may offer an opportunity to discuss nested categories of shapes: a square is a “special” rhombus, so if a rhombus is chosen, will students permit "square" in response? See Getting Started.

Before handing out the worksheet, you may also wish to discuss with students how they can work out areas of shapes on a dotted grid. 

The images below might provide a useful prompt - they demonstrate two alternative ways of working out the area of tilted squares:
  
   
         


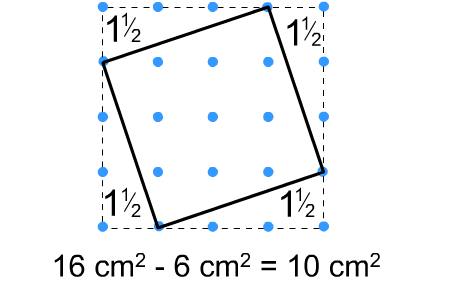
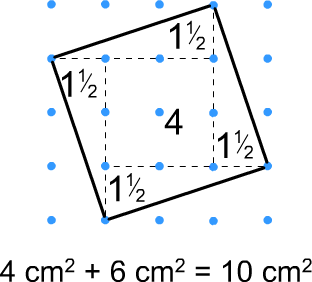
Lexy from QK Academy shared these ppt slides that she used with her class when they were working on this problem.

Key questions

What properties does a square / rectangle / parallelogram / kite / rhombus / trapezium / arrowhead have?
Is a square a special rectangle?
Is a rectangle a special parallellogram?
Is a rhombus a special kite?
 

Possible extension

These three problems provide suitable follow-up challenges:
Isosceles Triangles 
Triangles in a Square
Square it 

Possible support

Starting by playing Guess my Quad, in which students use properties of quadrilaterals to guess their opponent's shape using as few questions as possible, would offer an opportunity to clarify the properties of different quadrilaterals. 

Students could start with the shapes they are more confident with (perhaps squares, rectangles, parallellograms and kites) before tackling the rhombuses, trapezia and arrowheads.