Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Picture the Process I
Here are descriptions of eight real-world processes. For each, try to sketch a suitable graph. If you are not familiar with the background science, then try to use what you do know to reason through what a graph might look like.
You do not need to calculate or plot exact points, just sketch graphs that give the general shape.
As you produce your sketches, make a list of the features that you are considering.
Printable versions of these cards can be downloaded here
| Temperature of a cup of tea over time. | Height of the valve on a bicycle tyre as the bicycle moves forwards. |
| Height of a tennis ball thrown straight up and then caught. | Distance fallen by a parachutist jumping out of a plane. |
| Reading on the odometer (mile counter) of a car driving on a motorway. | Radius of a spherical balloon as it is inflated. |
| Volume of water remaining in a cup as water is sucked out through a straw. | Distance along a tape measure measured in inches compared with distance measured in metres. |
Once you have sketched graphs for some of the eight processes described, click on the following link to read a further question and move on further.
What features did you consider as you drew your sketches?
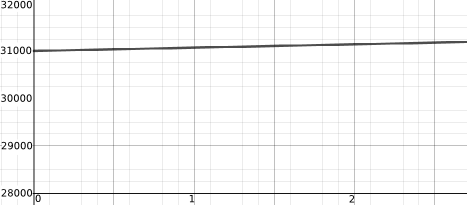
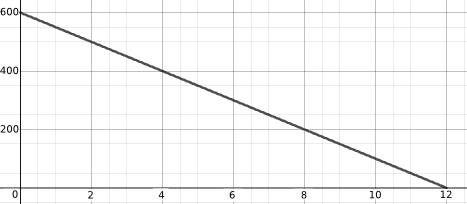
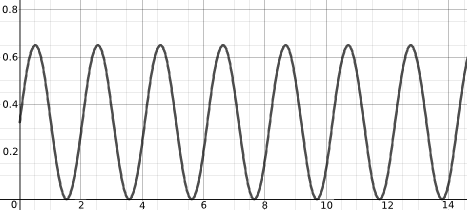
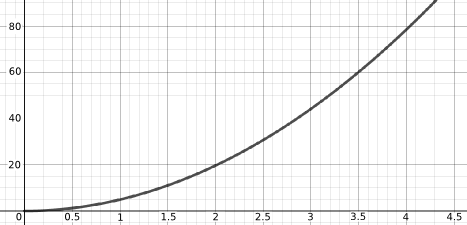
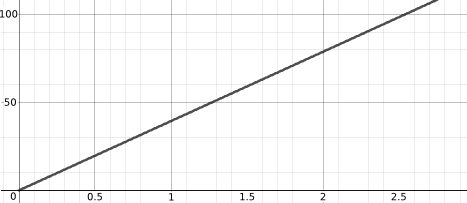
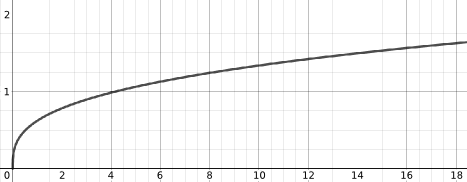
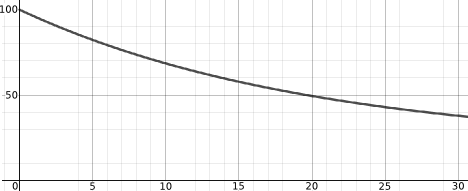
Below is a possible graph for each process (but they're muddled up). Can you match a graph to each process?
How do the graphs below compare to those you sketched? If you sketched something different, can you identify the assumptions that you made and those that might have led to the graphs below?
Printable versions of these cards can be downloaded here
 |
 |
 |
 |
 |
 |
 |
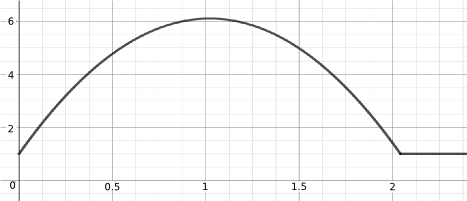 |
Hopefully you have now matched a graph to each process.
Can you suggest an equation for each process/graph pair?
When you have done this, click on the link below to continue.
Below is a possible equation for each process/graph pair (but they're muddled up). Can you match an equation to each process/graph?
Can you explain the numbers in these equations? They are all chosen to be physically sensible given suitable units. What might the units be for each process/graph/equation?
Printable versions of these cards can be downloaded here
| $y(x) = 10x - 4.9x^2 + 1$ | $y(x) = 600 - 50x$ |
| $y(x) = 39.37x$ | $y(x) = 4.9x^2$ |
| $y(x) = 0.6204\sqrt[3]{x}$ | $y(x) = 20 + 80e^{-0.05x}$ |
| $y(x) = 70x + 31000$ | $y(x) = 0.325\left(\sin(3.1x) + 1\right)$ |
Underground Mathematics is hosted by Cambridge Mathematics. The project was originally funded by a grant from the UK Department for Education to provide free web-based resources that support the teaching and learning of post-16 mathematics.
Visit the site at undergroundmathematics.org to find more resources, which also offer suggestions, solutions and teacher notes to help with their use in the classroom.
You may also like
Powerful Quadratics
This comes in two parts, with the first being less fiendish than the second. It’s great for practising both quadratics and laws of indices, and you can get a lot from making sure that you find all the solutions. For a real challenge (requiring a bit more knowledge), you could consider finding the complex solutions.
Discriminating
You're invited to decide whether statements about the number of solutions of a quadratic equation are always, sometimes or never true.
Factorisable Quadratics
This will encourage you to think about whether all quadratics can be factorised and to develop a better understanding of the effect that changing the coefficients has on the factorised form.


