Skip over navigation
Weida from Churston Ferrers Grammar School has given very thorough explanations for why some of the physical processes have the equations and the graphs that they do, and has also interpreted what the numbers on the graphs mean in terms of physical quantities.
Radius of a spherical balloon as it is inflated
We assume that the balloon is being inflated at a constant rate i.e. the volume of the balloon increases steadily with time.
Let $V$ be the volume of the balloon, $t$ the time elapsed since we started inflating the ballon and $r$ the radius of the balloon. From the assumption, $ V \propto t$. Also we know that the volume of a sphere is given by $V = \frac{4}{3} \pi r^3$ so $V \propto r^3$. Therefore $ t \propto r^3$ so for some constant $A$
$$ r = A \sqrt[3]{t} $$
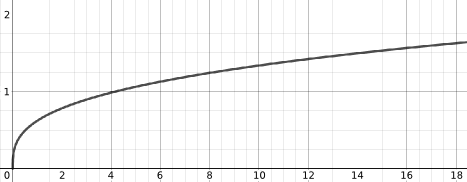
The equation given that matches this is $y(x) = 0.62043 \sqrt[3]{x}$.
Let us consider what the constant $A=0.62043$ represents. In $V \propto t$, the constant of proportionality is the volume of air put into the ballon per unit time, let's call this $p$. So
$V = p t = \frac{4}{3} \pi r^3 = \frac{4}{3} \pi A^3 t $
So $ p = \frac{4}{3} \pi A^3 = \frac{4}{3} \pi (0.62043)^3 = 1.00$ (3sf).
After 4 units of time on the graph the radius = 1 unit. So perhaps the units of time are seconds and 1 unit = 5 cm for the radius, in which case this would mean that every second $1 \times 5^3 = 125 \text{cm}^3$ of air was put into the balloon.
Height of the valve on a bicycle tyre as the tyre moves forwards
We assume that the wheel rotates at a constant rate, and that the bicylce is travelling horizontally. As the bicycle travels forwards, if we ignore the linear mostion of the valve in the direction that the bicycle is travelling, the valve is essentially tracing out a circle (see the sketch below)
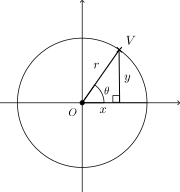
Let $V=(x,y)$ be the position of the valve. When $V$ has turned through an angle of $\theta$ anticlockwise from the x-axis, looking at the right-angled triangle drawn, we see that $y=r \sin{\theta}$.
Thinking back to the bicycle, y is the height of the valve above the height of the centre of the tyre, and $r$ is the radius of the tyre. We may wish to convert the height above the centre of the tyre $y$ to the height of the valve above the ground $H$, by adding $r$.
Also as the speed is constant we can say that $\theta = k t$ where $k$ is some constant and $t$ is time. Combining this we have that
$$ H = r \sin{k t} + r $$
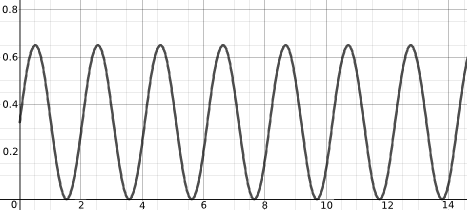
The given equtaion that this matches is $y(x) = 0.325 (\sin (3.1 x) +1)$. Comparing with $H =r \sin{k t} + r$ we see that $r=0.325$. As this represents the radius of the tyre, the unit is likely to be metres.
Can anyone see where the constant $3.1$ comes from if the x-axis represents distance the bicycle has travelled rather than time (and the angle is in radians)?
Temperature of a cup of tea over time
We assume that the rate at which the temperature decreases is proportional to the difference in temperature between the cup of tea and the room. So if $T$ represents the temperature of the tea and $t$ represents time, and room temperature is $20^{\circ}C$, then $-\frac{dT}{dt} \propto (T-20)$. This means, approximately, that the higher the temperature the faster the temperature decreases. On a graph of T against t, for smaller values of t, the gradient would be steeper.
From this we may set up a differential equation and solve it to find temperature as a function of time:
$$-\frac{dT}{dt} = k (T-20)$$
where $k$ is some positive constant.
Separating the variables we have
$$\frac{1}{T-20} \frac{dT}{dt} = -k $$
Integrating with respect to t,
$$ \int \frac{1}{T-20} \mathrm{d}T = \int -k \mathrm{d}t $$
$$ \ln{(T-20)} = -k t + c$$
Changing to exponential notation
$$T = 20 + e^{-k t + c} = 20 +A e^{-kt}$$
where $A$ is some constant.
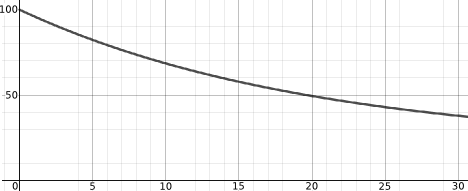
The equation given that matches this is $ y(x) = 20 + 80 e^{-0.05 x} $. The units of temperature for the y-axis was probably degrees celcius implying that the tea starts at $100^{\circ}C$ and ends up eventually at $20^{\circ}C$. It is likely that the unit for $x$ is minutes because after 30 minutes it is likely that the temperature would be $y(x) = 20 + 80 e^{-0.05 \times 30} \approx 38^{\circ}C$
Can anyone explain the graphs and equations behind any of the other processes?
Picture the Process I
Weida from Churston Ferrers Grammar School has given very thorough explanations for why some of the physical processes have the equations and the graphs that they do, and has also interpreted what the numbers on the graphs mean in terms of physical quantities.
Radius of a spherical balloon as it is inflated
We assume that the balloon is being inflated at a constant rate i.e. the volume of the balloon increases steadily with time.
Let $V$ be the volume of the balloon, $t$ the time elapsed since we started inflating the ballon and $r$ the radius of the balloon. From the assumption, $ V \propto t$. Also we know that the volume of a sphere is given by $V = \frac{4}{3} \pi r^3$ so $V \propto r^3$. Therefore $ t \propto r^3$ so for some constant $A$
$$ r = A \sqrt[3]{t} $$
The equation given that matches this is $y(x) = 0.62043 \sqrt[3]{x}$.
Let us consider what the constant $A=0.62043$ represents. In $V \propto t$, the constant of proportionality is the volume of air put into the ballon per unit time, let's call this $p$. So
$V = p t = \frac{4}{3} \pi r^3 = \frac{4}{3} \pi A^3 t $
So $ p = \frac{4}{3} \pi A^3 = \frac{4}{3} \pi (0.62043)^3 = 1.00$ (3sf).
After 4 units of time on the graph the radius = 1 unit. So perhaps the units of time are seconds and 1 unit = 5 cm for the radius, in which case this would mean that every second $1 \times 5^3 = 125 \text{cm}^3$ of air was put into the balloon.
Height of the valve on a bicycle tyre as the tyre moves forwards
We assume that the wheel rotates at a constant rate, and that the bicylce is travelling horizontally. As the bicycle travels forwards, if we ignore the linear mostion of the valve in the direction that the bicycle is travelling, the valve is essentially tracing out a circle (see the sketch below)
Let $V=(x,y)$ be the position of the valve. When $V$ has turned through an angle of $\theta$ anticlockwise from the x-axis, looking at the right-angled triangle drawn, we see that $y=r \sin{\theta}$.
Thinking back to the bicycle, y is the height of the valve above the height of the centre of the tyre, and $r$ is the radius of the tyre. We may wish to convert the height above the centre of the tyre $y$ to the height of the valve above the ground $H$, by adding $r$.
Also as the speed is constant we can say that $\theta = k t$ where $k$ is some constant and $t$ is time. Combining this we have that
$$ H = r \sin{k t} + r $$
The given equtaion that this matches is $y(x) = 0.325 (\sin (3.1 x) +1)$. Comparing with $H =r \sin{k t} + r$ we see that $r=0.325$. As this represents the radius of the tyre, the unit is likely to be metres.
Can anyone see where the constant $3.1$ comes from if the x-axis represents distance the bicycle has travelled rather than time (and the angle is in radians)?
Temperature of a cup of tea over time
We assume that the rate at which the temperature decreases is proportional to the difference in temperature between the cup of tea and the room. So if $T$ represents the temperature of the tea and $t$ represents time, and room temperature is $20^{\circ}C$, then $-\frac{dT}{dt} \propto (T-20)$. This means, approximately, that the higher the temperature the faster the temperature decreases. On a graph of T against t, for smaller values of t, the gradient would be steeper.
From this we may set up a differential equation and solve it to find temperature as a function of time:
$$-\frac{dT}{dt} = k (T-20)$$
where $k$ is some positive constant.
Separating the variables we have
$$\frac{1}{T-20} \frac{dT}{dt} = -k $$
Integrating with respect to t,
$$ \int \frac{1}{T-20} \mathrm{d}T = \int -k \mathrm{d}t $$
$$ \ln{(T-20)} = -k t + c$$
Changing to exponential notation
$$T = 20 + e^{-k t + c} = 20 +A e^{-kt}$$
where $A$ is some constant.
The equation given that matches this is $ y(x) = 20 + 80 e^{-0.05 x} $. The units of temperature for the y-axis was probably degrees celcius implying that the tea starts at $100^{\circ}C$ and ends up eventually at $20^{\circ}C$. It is likely that the unit for $x$ is minutes because after 30 minutes it is likely that the temperature would be $y(x) = 20 + 80 e^{-0.05 \times 30} \approx 38^{\circ}C$
Can anyone explain the graphs and equations behind any of the other processes?
You may also like
Powerful Quadratics
This comes in two parts, with the first being less fiendish than the second. It’s great for practising both quadratics and laws of indices, and you can get a lot from making sure that you find all the solutions. For a real challenge (requiring a bit more knowledge), you could consider finding the complex solutions.
Discriminating
You're invited to decide whether statements about the number of solutions of a quadratic equation are always, sometimes or never true.
Factorisable Quadratics
This will encourage you to think about whether all quadratics can be factorised and to develop a better understanding of the effect that changing the coefficients has on the factorised form.