Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Towering Trapeziums



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
T. Hakim from Annie Gale School in Canada defined a new point, $M$, as the midpoint of $CD$.
You had to understand the pattern of the triangles and the relationship between triangles $ABO$ and $ODM$.
This relation states that because the hypotenuse of $ODM$ is the same as $ABO$, and because it is an isosceles right triangle (so the other sides are the same),
$$ABO = ODM$$
With this information, I was able to figure out the rest of the triangle, and even the $n^\text{th}$ trapezium with these steps!
1) last full smaller-looking triangle = half of the next triangle (in the first case, $OAB=\frac12OCD$)
2) multiply half-triangle by two to create full triangle (therefore $2\times$ size of the previous triangle) (in the first case, $OCD$ has area $2\times$ area of $OAB$ which is $2\times1=2$)
3) subtract larger from smaller to get trapezium (in the first case, $2-1=1$)
After solving 4 trapeziums, I noticed a pattern, which was doubling the last trapezium's size, which made it a lot easier to solve.
next trapezium = $2\times$ last trapeizum
Matt from Swindon Academy in the UK, Amrit from Hymers College in the UK and Pablo from King's School Alicante in Spain considered the sides $OA$ and $OB$ as the base and height of triangle OAB, since the angle between them is $90^\text o$.
 Amrit said:
Amrit said:Let $OA=OB=x$, then
$\frac12x^2=1$
Therefore $x^2=2\Rightarrow x=\sqrt2$
Let $AB=OC=y$, then by the Pythagorean theorem,
$2x^2=y^2$
Plugging in the value of $x$, we have $2\times2=y^2\Rightarrow y=2$
The area of triangle $OCD$ is $\frac12y^2=2$. Therefore the area of the trapezium is $2-1=1$.
Pablo and Matt continued using the same methods to find the areas of the next trapeziums and generalise. This is Pablo's work:
TRAPEZIUM 2
$OC = OD = 2$
$CD^2 = 2^2 + 2^2$
$CD^2 = 8$
$CD =OE= 2\sqrt2$
Area of $OEF = 2\sqrt2 \times2\sqrt2\times \frac12= 4$
Area of trapezium $CDFE = $Area$ OEF - $Area$ OCD = 4 - 2 = 2 $ units$^2$
TRAPEZIUM 3
$OE = OF = 2\sqrt2$
$EF^2 = OE^2+ OF^2 = (2\sqrt2)^2+(2\sqrt2)^2$
$EF^2 = 8 + 8$
$EF = 4$
$OG = 4$
Area $OGH = 4\times4\times\frac12 = 8$ units$^2$
Area of trapezium $EFHG = $Area$ OGH - $Area$ OEF = 8 - 4 = 4 $ units$^2$
NTH TRAPEZIUM
For the first trapezium, $ABDC$, we had to subtract the area of the triangle $OAB$ from triangle $OCD$. If we call $OA$ the 'first' length, $OC$ is the 'second' length.
$OA = \sqrt{2^1}$ [first]
$OC = 2 = \sqrt{2^2}$ [second]
this continues for $OE$ and $OG$
So the area of the trapezium was $\frac12 OC^2 - \frac12 OA^2$
If instead of $OA$ and $OC$ we had the $n^\text{th}$ and the $(n+1)^\text{th}$ lengths, we can
say that:
the area of the $n^\text{th}$ trapezium
$= \frac12\left(\sqrt{2^{n+1}}^2\right) - \frac12\left(\sqrt{2^n}^2\right)$
$= \frac12 \times 2^{n+1} - \frac12\times 2^n$
$= 2^n - 2^{n-1}$
$= 2^n\left(1 - 2^{-1}\right)$
$= 2^n\left(1 - \frac12\right)$
$= 2^n\left(\frac12\right)$
$= 2^n\left(2^{-1}\right)$
$= 2^{n-1}$
Amrit used similarity to find the area of the $n^\text{th}$ trapezium:
It is clear to see that all the trapeziums are similar.
Say $OA$ was length $y_0$ and $OC$ was length $y_1$, then $y_1=\sqrt2y_0$
If $CD=OE$ was $y_2$, then $y_2=\sqrt2y_1$
If we call $y_n$ the length of the $n^\text{th}$ parallel line, then $y_{n+1}=\sqrt2 y_n$
So $\dfrac{y_{n+1}}{y_n}=\sqrt2$
This is the scale factor between the sides of adjacent trapezia, so the area factor between them is $2$. We now need to find the area of the first trapezia to find a formula for the others.
The area of the first trapezium was $1$, so the area of the second trapezium is $2$, and the area of the third trapezium is $4$, and the area of te fourth trapezium is $8$, so
the area of the $n^\text{th}$ trapezium is $2^{n-1}$.
Guruvignesh and Adithya, also from Hymers College, considered the base and height of the triangle as horizontal and vertical.
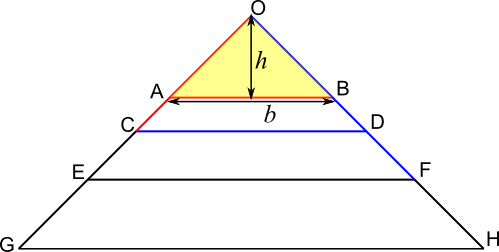 Firstly, we must use the formula for the area of a triangle: $\frac12b\times h=1\Rightarrow b\times h=2$
Firstly, we must use the formula for the area of a triangle: $\frac12b\times h=1\Rightarrow b\times h=2$Then, they observed that splitting triangle OAB in half along the height $h$ creates two more right-angled triangles. The new triangles are also isosceles, so $\frac12b=h$.
So $b=AB=2$ and $h=1$ since the area is $1$ square unit.
Given that $AB=OC$, $OC= 2$ and similarly $OD=2$ since $OCD$ is a similar triangle to that of triangle $OGH$. Using the relative sizes of a 45 degree right angled triangle: $1:1: \sqrt2$ (this comes from $1^2+1^2=(\sqrt2)^2$),
$CD:OC=\sqrt2:1$
So $CD=2\sqrt2$
Because we now know that the height of each right angled isosceles triangle in this shape is half the base, the height of triangle $OCD$ is $2^\frac12$.
Thus, the height of the trapezium is $2^{\frac12} - 1$.
$$\begin{split}A&=\frac{a+b}2h\\
&=\frac{AB+CD}2\left(2^{\frac12} - 1\right)\\
&=\frac{2\sqrt2+2}2\left(2^{\frac12} - 1\right)\\
&=\left(\sqrt2+1\right)\left(\sqrt2-1\right)\\
&=1\end{split}$$ So the area is $1$ square unit.
For the next trapezium,
$OE = 2\sqrt2$
Using the relative sizes ratio for a right angled isosceles triangle:
$EF = 4$
Therefore the height of triangle $OEF$ is $2$
But the height of the trapezium is $2 - \sqrt2$
Area of trapezium $CDFE:$
$$\begin{split}A &= \frac12 (a + b) h\\
&= \frac12 (EF + CE) (2 - \sqrt2)\\
&= \frac12 (4 + 2\sqrt2) (2 - \sqrt2)\\
&=(2+\sqrt2)(2-\sqrt2)
&= 2\end{split}$$
Adithya and Guruvignesh both created a table to show how the sequence continues:
| Term | 1 | 2 | 3 | 4 | 5 |
| Area | 1 | 2 | 4 | 8 | 16 |
And they spotted that the $n^\text {th}$ term is equal to $2^{n-1}$.
The reason for this is because each trapezium is a similar shape to the one before. So, if we increase by scale factor $\sqrt2$ (due to the relative sizes of a right angled isosceles triangle), the area factor will increase by 2. Because $AF = SF^2$.
You may also like
At a Glance
The area of a regular pentagon looks about twice as a big as the pentangle star drawn within it. Is it?
Six Discs
Six circular discs are packed in different-shaped boxes so that the discs touch their neighbours and the sides of the box. Can you put the boxes in order according to the areas of their bases?
Equilateral Areas
ABC and DEF are equilateral triangles of side 3 and 4 respectively. Construct an equilateral triangle whose area is the sum of the area of ABC and DEF.

