Isosceles Seven

Why do this problem?

This problem is an "angle chase" problem, which requires knowledge of angles in an isosceles triangle, and angles on a straight line.  It requires students to have the ability to express the problem algebraically, and to then solve the equation that emerges.

Students are then challenged to think more generally.

Possible approach:

This problem featured in the NRICH Secondary webinar in April 2022.

Project the problem onto a board and ask students which lengths are equal.  Mark these onto the diagram and ask students how many isosceles triangles they can find (and the names of them!).

Mark on angle $BAC$ as $x$.  Ask students if there are any other angles equal to $x$.  Also ask students if they know anything about any of the other angles.

Possible support:

You could start by asking students to consider a simpler case, such as the one below, or an isosceles triangle made up of just two isosceles triangles, $ABC$ and $BCD$:

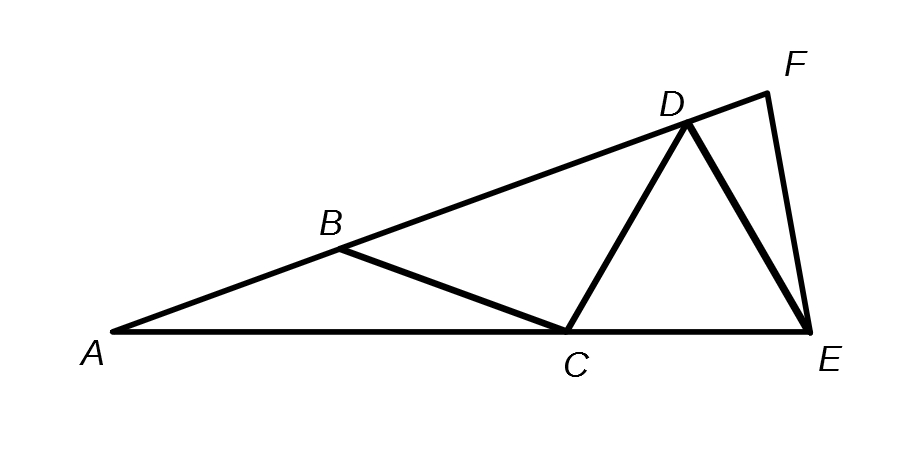
Possible extension:

Can you construct similar isosceles triangles, made up of a number of smaller isosceles triangles, in which the angles are all whole numbers? 

If the isosceles triangle is composed of $n$ isosceles triangles, and angle $BAC = x$, what are the values of the other angles of the triangle?