Isosceles Seven

Yihuan from Pate's Grammar School in the UK, Ci Hui Minh Ngoc from Kelvin Grove State College (Brisbane) in Australia and Boyi from Wellington College International Shanghai found the angles in triangle $AHI.$ This is Yihuan's explanation with Boyi's diagram.

If we name angle $BAC$ angle $x$, we can say that angle $ABC$ is equal to $180-2x$ as base angles in an isosceles triangle are equal and angles in a triangle add up to $180$ degrees.  Then angle $DBC$ must equal $2x$ as the exterior angle is equal to the sum of the two interior angles. So angle $BCD$ must equal $180-4x$ because base angles in an isosceles triangle are equal and angles in a triangle add up to $180$ degrees. Then angle $DCE$ is equal to $3x$ as angles $BCA+BCD+DCE$ add up to $180$ as angles on a straight line sum to $180$ degrees, and we know $BCA$ and $BCD,$ so if we subtract them then we are left with $DCE=3x.$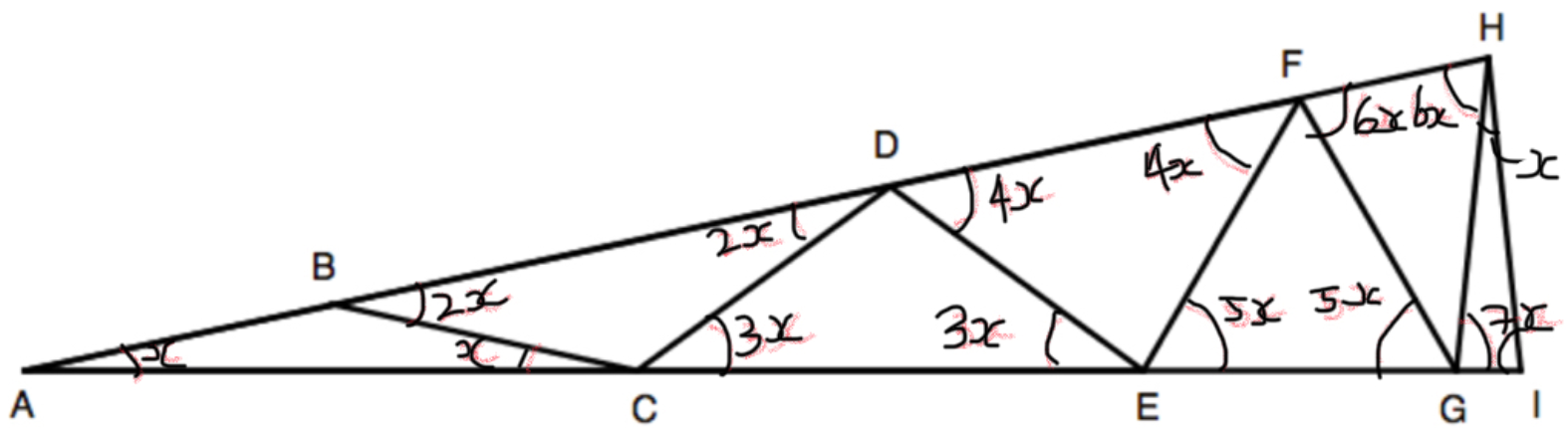

Then $CDE=180-6x$ for the same reason that $BCD=180-4x$ and $FDE=4x$ for the same reason that $DCE=3x.$ Here we can see that there is a repeating pattern that the base angles in each isosceles triangle going upwards is increase by $x$ each time. If we follow this pattern up to the top of the 'main' isosceles triangle then we get that angle $GIH=7x.$ Since triangle $AHI$ is isosceles then $AHI$ must also be $7x$ as base angles in an isosceles triangle are equal. As angles in a triangle sum to $180$ degrees then we get $15x=180$ so $x=12$ degrees. So angle $HAI$ is $12$ degrees and angles $AHI$ and $AIH$ are both $84$ degrees.

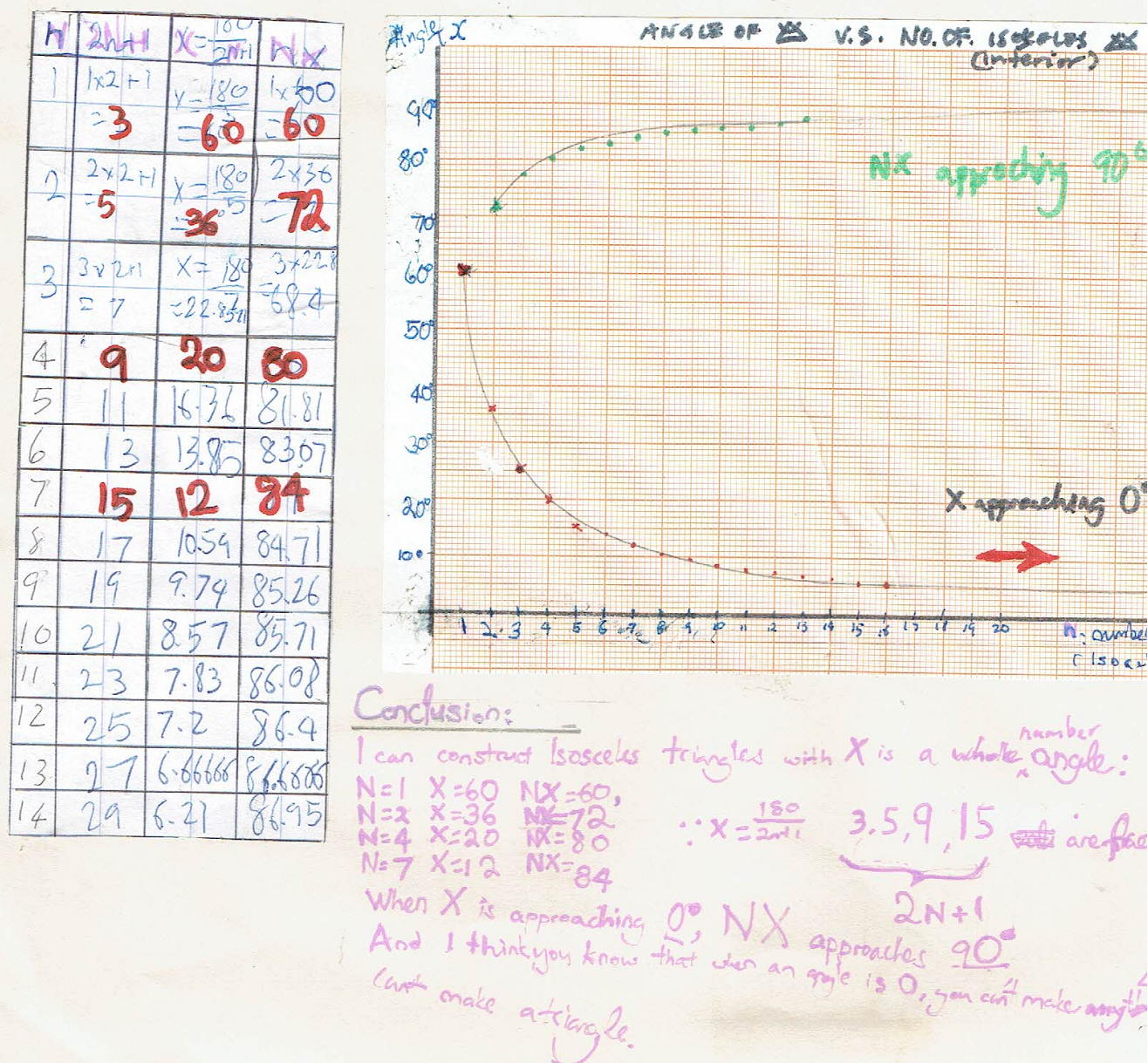
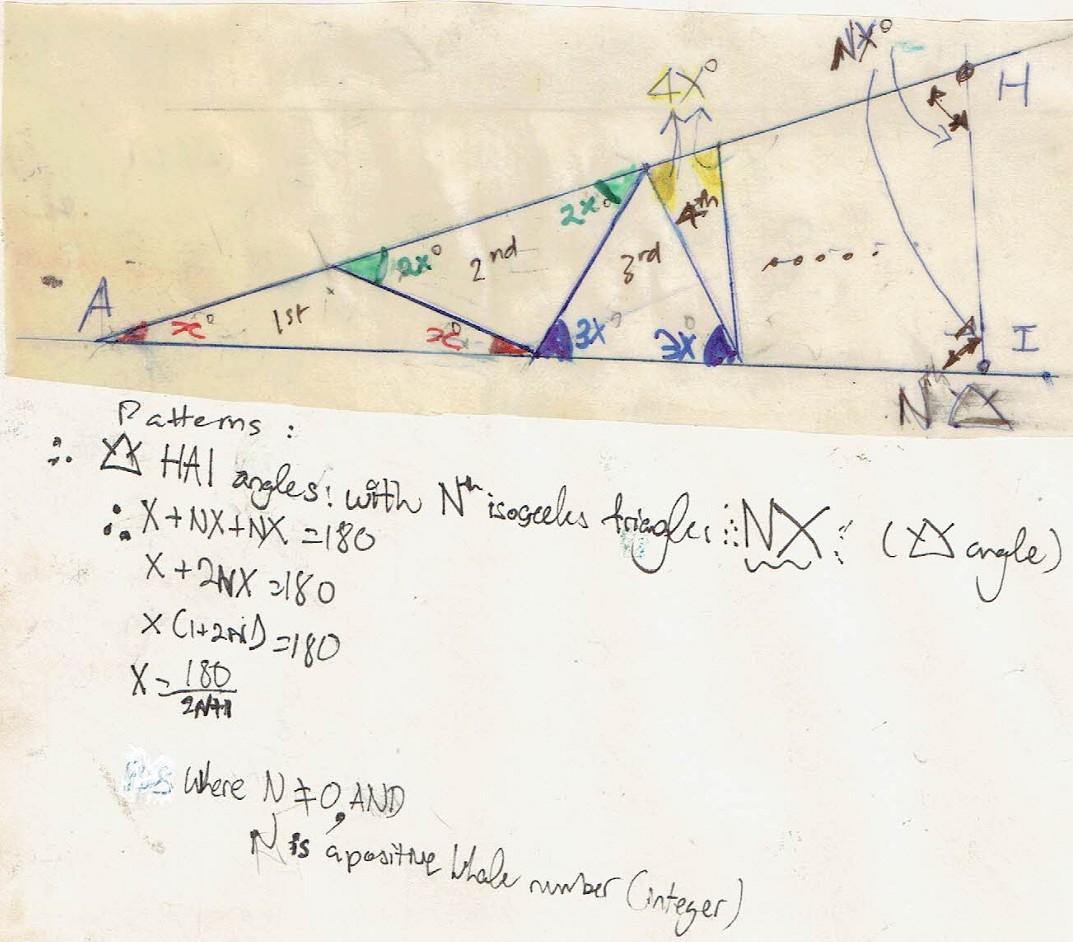
Yihuan, Boyi and Ci Hui Minh Ngoc extended this to $n$ triangles. This is Ci Hui Minh Ngoc's work:

From here, Boyi found a triangle made up of a number of smaller isosceles triangles in which the angles are all whole numbers:

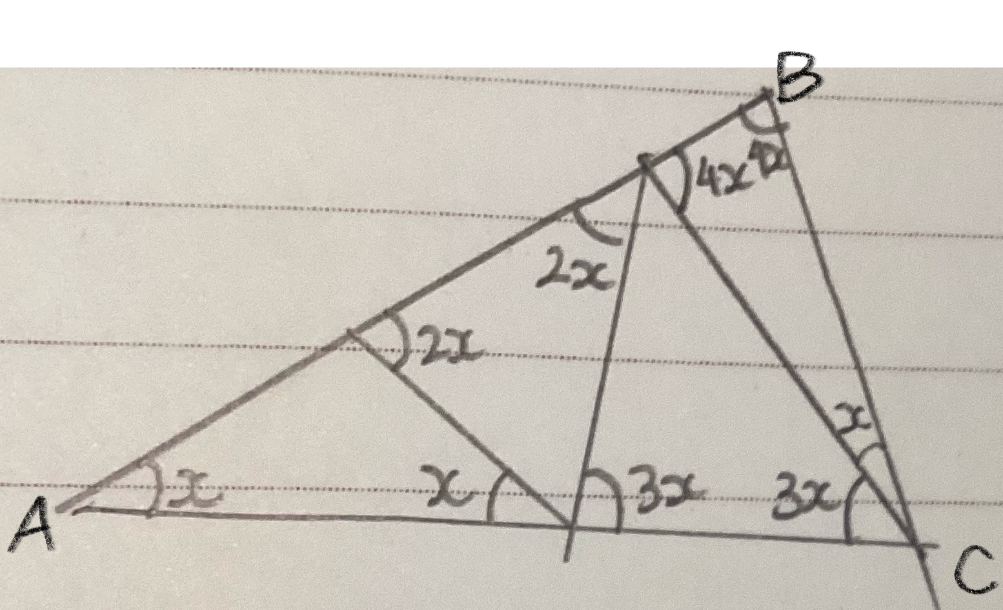
$180$ degrees $- 8x (4x + 4x) = x$
$180=9x$
$x=20$

Therefore angles $ABC$ and $ACB$ are all $80$ degrees with $BAC$ as $20$ degrees.

Yihuan explained how to find all of the possible whole-number angles in isosceles triangles made in this way:

As long as $180$ is divisible by $2n+1$ then $x$ will be a whole number and therefore all the angles will be a whole number as $n$ will be a whole number and their product will be whole as well. An example of a possible value of $n$ which fulfills the conditions would be $n=4.$

Ci Hui Minh Ngoc used a table and graph to explore the sizes of the angles for different values of $n.$ Click on the image to see a larger version.

There is one more value of $n$ which gives a whole number value for $x$. Can you find it?