An Equilateral Triangular Problem
An Equilateral Triangular Problem printable sheet
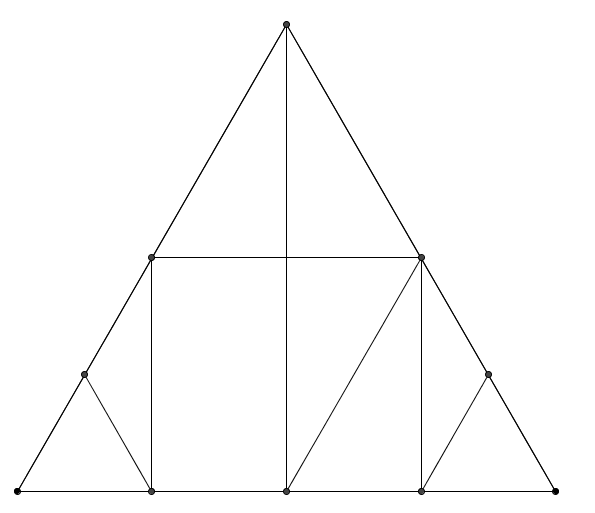
The picture above shows an equilateral triangle, with lines drawn between various midpoints.
Have a go at printing out this triangle, and cutting along the lines to make nine smaller shapes.
What are the angles in each of your smaller shapes?
If the area of the smallest equilateral triangle is one unit, what is the area of each of the other shapes?
We can take a collection of the smaller cut out areas and rearrange them to make different shapes.
Using the nine smaller shapes:
- How many different trapezia (which are not parallelograms) can you make?
- How many different parallelograms (which are not rectangles) can you make?
- How many different rectangles can you make?
- Which other quadrilaterals can you make?
You may find it useful to print out the figure.
You may also like
Linkage
Four rods, two of length a and two of length b, are linked to form a kite. The linkage is moveable so that the angles change. What is the maximum area of the kite?
Making Rectangles, Making Squares
How many differently shaped rectangles can you build using these equilateral and isosceles triangles? Can you make a square?
The Cyclic Quadrilateral
This gives a short summary of the properties and theorems of cyclic quadrilaterals and links to some practical examples to be found elsewhere on the site.