An Equilateral Triangular Problem

Why do this problem?

This problem can be used in a number of different ways - for students to think about angles, area, or properties of polygons.
 

Possible approach

Show students the image from the problem, or hand out this worksheet.
  
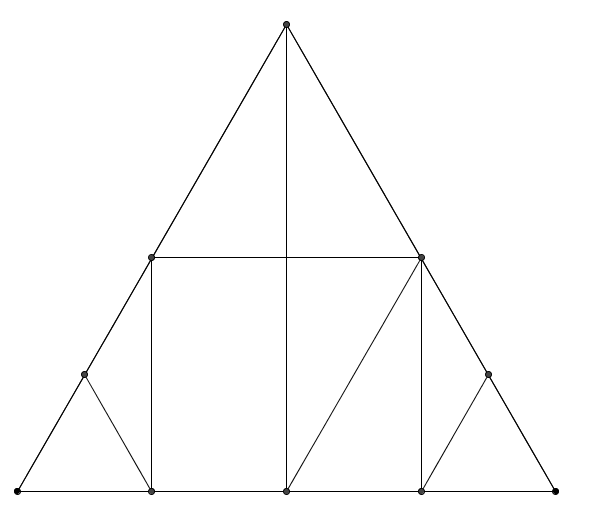
"The image was made by taking an equilateral triangle and finding and joining some of its midpoints. Can you work out the angles in the shape?"
Give students a little time to find the missing angles, then discuss the methods they used to work them out.

"Let's imagine that the area of the smallest equilateral triangle is 1 unit. Can you work out the areas of all the other pieces?"
Again, give the class some time to discuss the problem with a partner, and then bring the class together to discuss the reasoning they used to work out how the area of each piece compared with the area of the smallest equilateral triangle.

Next, invite the students to cut the triangle up into the nine smaller pieces to explore the following questions:

• How many different trapeziums (which are not parallelograms) can you make?
• How many different parallelograms (which are not rectangles) can you make?
• How many different rectangles can you make?
• Which other quadrilaterals can you make?

Students could record their working on isometric dotty paper.
As students are working, circulate and listen to their discussions to verify that they understand the properties of trapezia, parallelograms and rectangles. Look out for any examples that not all students have found, and draw attention to them in the final plenary.
 

Key questions

What angles/areas do you know?
How can you use the angles/areas you know to work out other angles/areas?
What properties does a trapezium/parallelogram/rectangle have?

Possible support

Guess my Quad

Possible extension

Completing Quadrilaterals