Skip over navigation
Centred Squares
Age 7 to 11
Challenge Level 
You may know about some number sequences like odd numbers, square numbers, triangular numbers, etc.
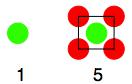
One you may not have come across before is to do with squares. The sequence starts with one and then four points are put around it in a square:
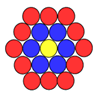
Because the shape is growing bigger with new layers added around the outside and the centre staying the same, the sequence 1, 5, ... is called Centred Squares.
Here's the start of the third layer, but it is not yet completed:
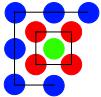
Can you see how to complete the third layer?
You can now make your own 4th Centred Square.
Rather than saying that, for example, the second centred square has five points, instead we could say that the second Centred Square number is 5.
Challenge 6
One you may not have come across before is to do with squares. The sequence starts with one and then four points are put around it in a square:
Because the shape is growing bigger with new layers added around the outside and the centre staying the same, the sequence 1, 5, ... is called Centred Squares.
Here's the start of the third layer, but it is not yet completed:
Can you see how to complete the third layer?
You can now make your own 4th Centred Square.
Rather than saying that, for example, the second centred square has five points, instead we could say that the second Centred Square number is 5.
Challenge 1
Find the first five Centred Square numbers.
Challenge 2
Without making the 6th, 7th, 8th Centred Square numbers, find the 9th Centred Square number.
Explain how you did this.
Explain how you did this.
Challenge 3
Using some of the nine Centred Square numbers, make a total of 211 or 212 or 213.
You can only use any Centred Square number once in any addition.
Explain how you chose the Centred Square numbers to use in your total.
You can only use any Centred Square number once in any addition.
Explain how you chose the Centred Square numbers to use in your total.
Challenge 4
Using your solution to Challenge 3, work out a way of making the other two totals.
Explain how you did this.
Explain how you did this.
Challenge 5
Find other ways of making those three totals using just the first nine Centred Square numbers.
Remember you can only use any Centred Square number once in any addition.
Remember you can only use any Centred Square number once in any addition.
Challenge 6
Finally, find ALL the ways of making 211, 212 and 213 and be able to convince others that you have found them all.
You may also like
Counting Counters
Take a counter and surround it by a ring of other counters that MUST touch two others. How many are needed?
Cuisenaire Squares
These squares have been made from Cuisenaire rods. Can you describe the pattern? What would the next square look like?
Doplication
We can arrange dots in a similar way to the 5 on a dice and they usually sit quite well into a rectangular shape. How many altogether in this 3 by 5? What happens for other sizes?