Centred Squares

Thank you to everybody who sent in their solutions to this problem. Max, Alice, Catherine and Finn from Strand on the Green Junior School in the UK sent in this very clear solution to the first few challenges:

Challenge 1
We drew the first 5 centred squares to find them.
They are 1, 5, 13, 25 and 41.

Challenge 2
We noticed that to get the next centred square you add four more each time.

The 9th number would be 1 + 4 + 8 + 12 + 16 + 20 + 24 + 28 + 32
which is the same as 1 + (1 x 4) + (2 x 4) + (3 x 4) + (4 x 4) + (5 x 4) + (6 x 4) + (7 x 4) + (8 x 4)

If you add them together that makes 1 + (36 x 4) = 145

Challenge 3
We worked out the first 9 centred square numbers are 1, 5, 13, 25, 41, 61, 85, 113, 145
Max then carried on with the challenges.
He started with 145 because it is closest to the total.
211  - 145 = 66
You can make 66 using 61 + 5 or 41 + 25 so 211 is 145 + 61 + 5 or 145 + 41 + 25

Challenge 4
To get 212 you can just add 1 so 145 + 61 + 5 + 1 or 145 + 41 + 25 + 1

213 - 145 = 68 and we couldn't find a way to make 68 so tried starting with 113 instead.
213 - 113 = 100
100 - 61 = 39
39 - 25 = 14
1 + 13 + 25 + 61 + 113 = 213

Can you follow their reasoning to see how they worked out that last total?

We also received lots of solutions from the children at Ganit Kreeda in Vicharvatika, India. Well done to Sowjanya, Avyukt Ag., Adhrit, Achyuth, Ridhit, Niveditha, Pranit, Taran, Avyukt As., Rudransh, Abhiram, Nishika, Vidyut, Vishnu and Bhuvana for thinking so carefully about this!

Avyukt, Achyuth, Niveditha and Rudransh also noticed that to get the next Centred Square number we add four more each time, and they used this picture to work out why this happens:

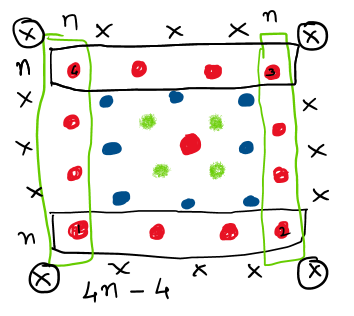
In this picture, 'n' represents the number of new dots added along one side of the Centred Square number. For the second Centred Square number, that will be 2, and for the third Centred Square number, that will be 3, etc.

Niveditha used algebra to explain the pattern:

The number of dots added extra in the new figure is 2n + 2(n - 2) = 2n + 2n – 4 = 4n - 4 = 4(n - 1)

The other approach to count extra dots is: 4n – 4(corner dots) = 4(n - 1).

Niveditha is saying that each time, we are adding nearly 4 lots of n to the previous Centred Square number - but if we did that then we would count the corner dots twice, so we have to subtract 4. I think there might be another way of drawing this picture to show that we are always adding 4 lots of one less than n... Can you see a way of showing that in the picture above, the red dots added in the outer layer are four lots of three?

Vidyut, Sowjanya and Avyukt spotted a different pattern to help them solve Challenge 2:

Every Centred Square number except for 1 is sum of 2 consecutive square numbers. For example: 5=1+4, 13=4+9, 25=9+16

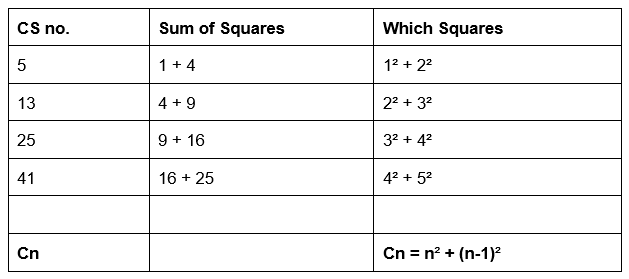
The children here are using 'n' and 'Cn' to represent general numbers, where 'n' can count which Centred Square number we are up to and 'Cn' can represent that Centred Square number. For example, with the third Centred Square number, n would be 3 and Cn would be 3² + 2². Can you see how this formula can help us work out the ninth Centred Square number?

The children used the following picture to think about why this pattern happens:

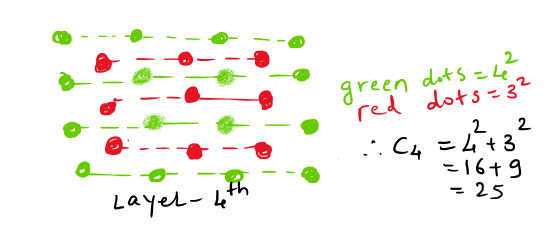
Using this picture, can you see why we add two square numbers together to get each Centred Square number?

The children worked collaboratively to solve Challenge 6:

Every Centred Square (CS) number is odd and ends in either 1 or 3 or 5.

A CS number always leaves a remainder 1 when divided by 4. 

Or in other words, a CS no. is 1 more than a multiple of 4.

As 211 leaves 3 as remainder when divided by 4, we need to use either 3 or 7 CS numbers to get 211.
Secondly, as all CS numbers end in 1 or 3 or 5, the way we can get 1 as the units place digit in a sum of 3 numbers is:

5+5+1 and 3+3+5

Using this logic, we tried all possible combinations and found:

211 = 5+61+145

       = 13+85+113

       = 25+41+145

212 = 1+5+61+145

       = 1+13+85+113

       = 1+25+41+145

       = 13+25+61+113

       = 25+41+61+85

213 = 1+13+25+61+113

       = 1+25+41+61+85

Thank you all for sharing your ideas with us!