Skip over navigation
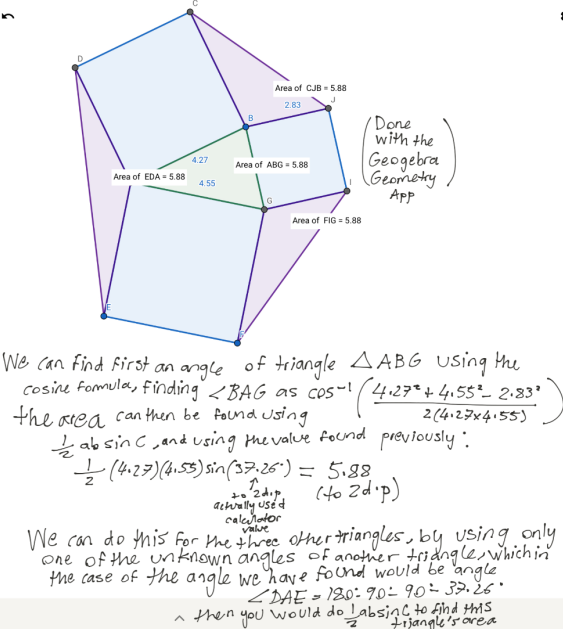
Mathula from Doha College in Qatar made some observations using GeoGebra. Mathula's work below includes finding the areas manually using the cosine rule
($a^2 = b^2 + c^2 - 2bc\cos A$) and the formula for the area of a triangle $A=\frac12 ab\sin C$.
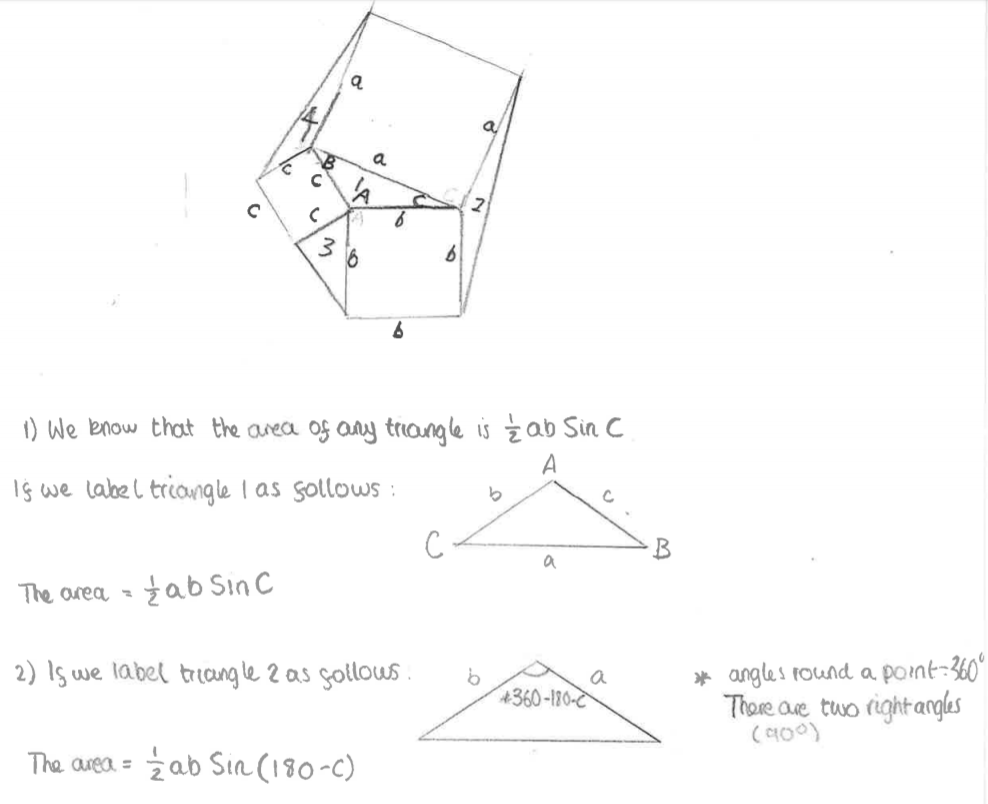
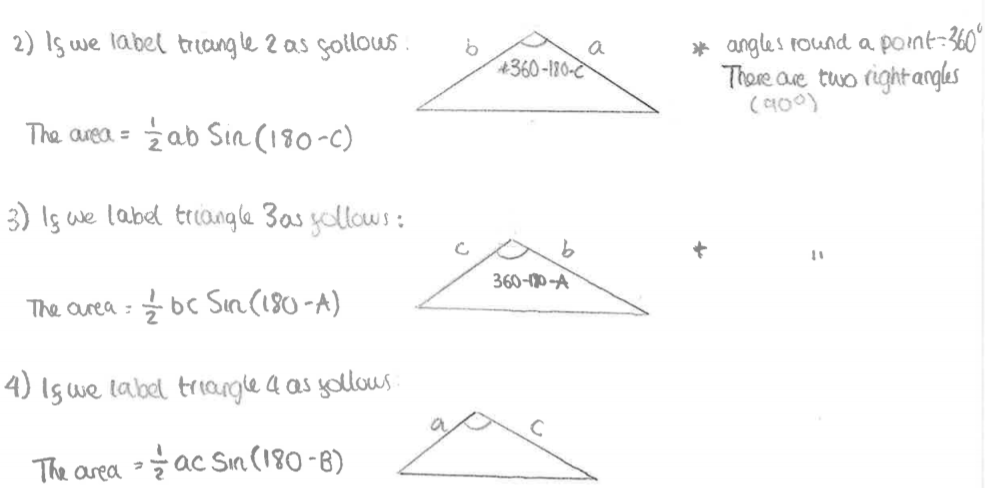
Beste and YiÄŸit from Amasya Åžehit Ferhat Ãœnelli Bilim Ve Sanat Merkezi in Turkey, Max, Ashwin, Jayden and Will and Jakob and Scott from Abingdon School in the UK and Mathula all proved that the four triangles have the same area using these two rules. This is Jakob and Scott's work:
This is Mathula's explanation of step 5:
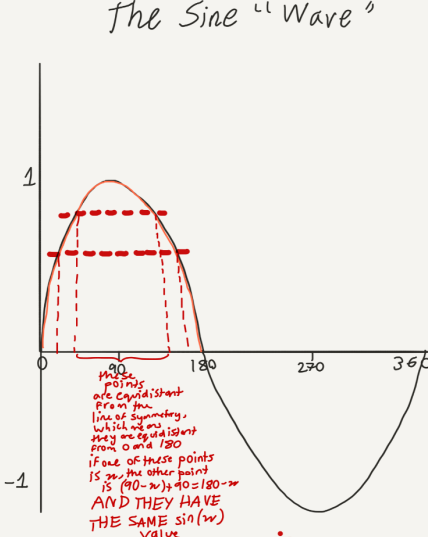
The sine wave has an axis of symmetry at 90, as $\sin{0}$ and $\sin{180}$ have the same value.
The red text says:
these points are equidistant from the line of symmetry, which means they are equidistant from $0$ and $180$
if one of these points is $x$, the other point is $(90-x)+90=180-x$ AND THEY HAVE THE SAME $\sin x$ VALUE
There is another method which the second interactivity in the Getting Started section can help you find.
Click to see the solution using this method.
The areas of each of the four triangles are the same. We can show this for triangles $ABC$ and $ADE$ by rotating the triangle $ADE$ through $90^{\circ}$ anticlockwise, so that $AD$ lies along $AC$ (the blue shaded triangle). Then $AB=AE'$, so $AC$ is a median of the triangle $BCE'$. Hence triangle $ABC$ has the same area as triangle $ACE'$ and therefore also the triangle $ADE$. (Or we can just notice that $BA=AE'$ and triangles $ABC$ and $ACE'$ have the same perpendicular height).
Beste and YiÄŸit, Max, Ashwin, Jayden and Will and Mathula used their result about the triangle to prove similar results about the quadrilateral and the triangle with two squares on one side. This is Beste and YiÄŸit's work on the quadrilateral:
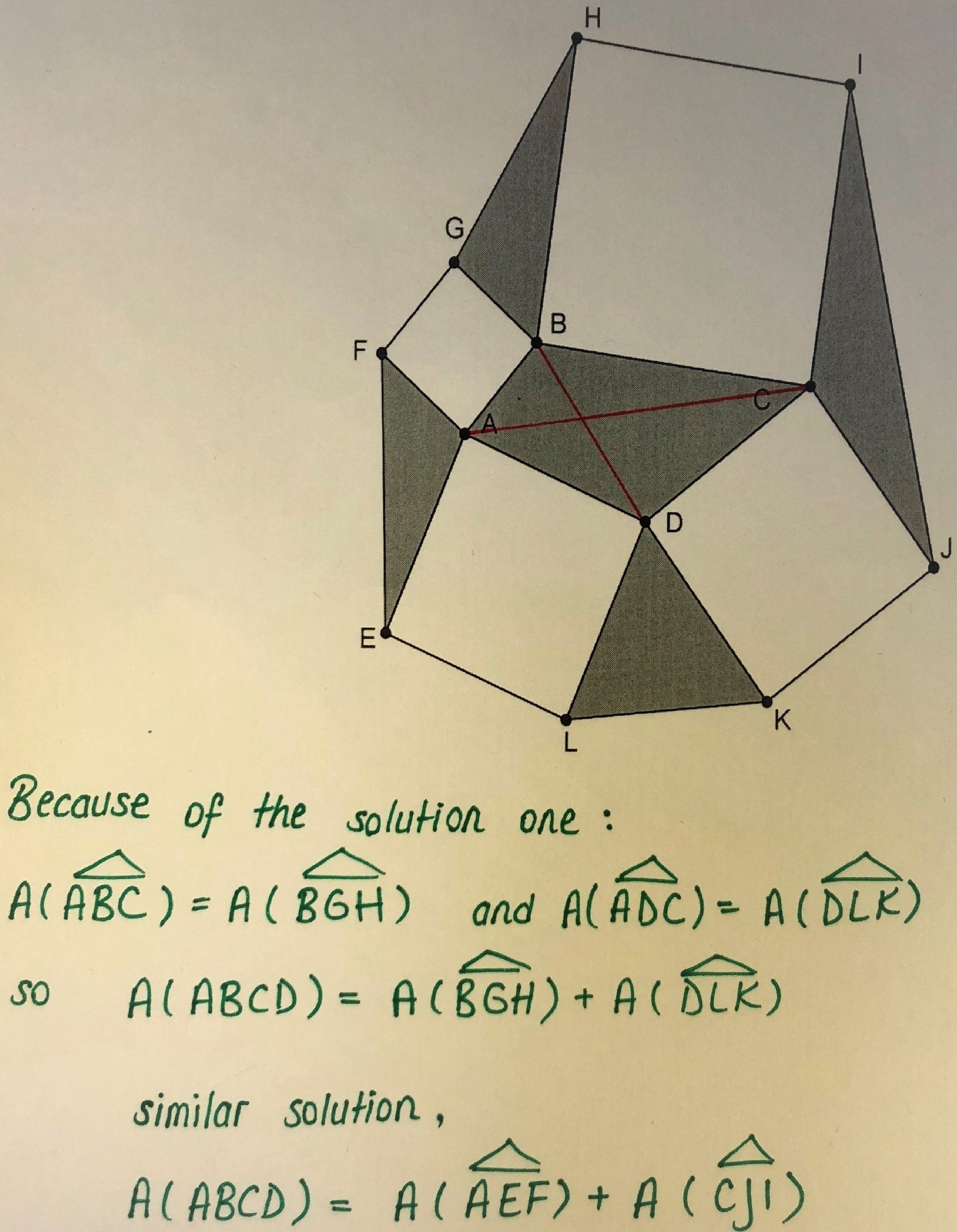
This Max, Ashwin, Jayden and Will's work on the triangle with two squares on one side, with Beste and YiÄŸit's diagram.
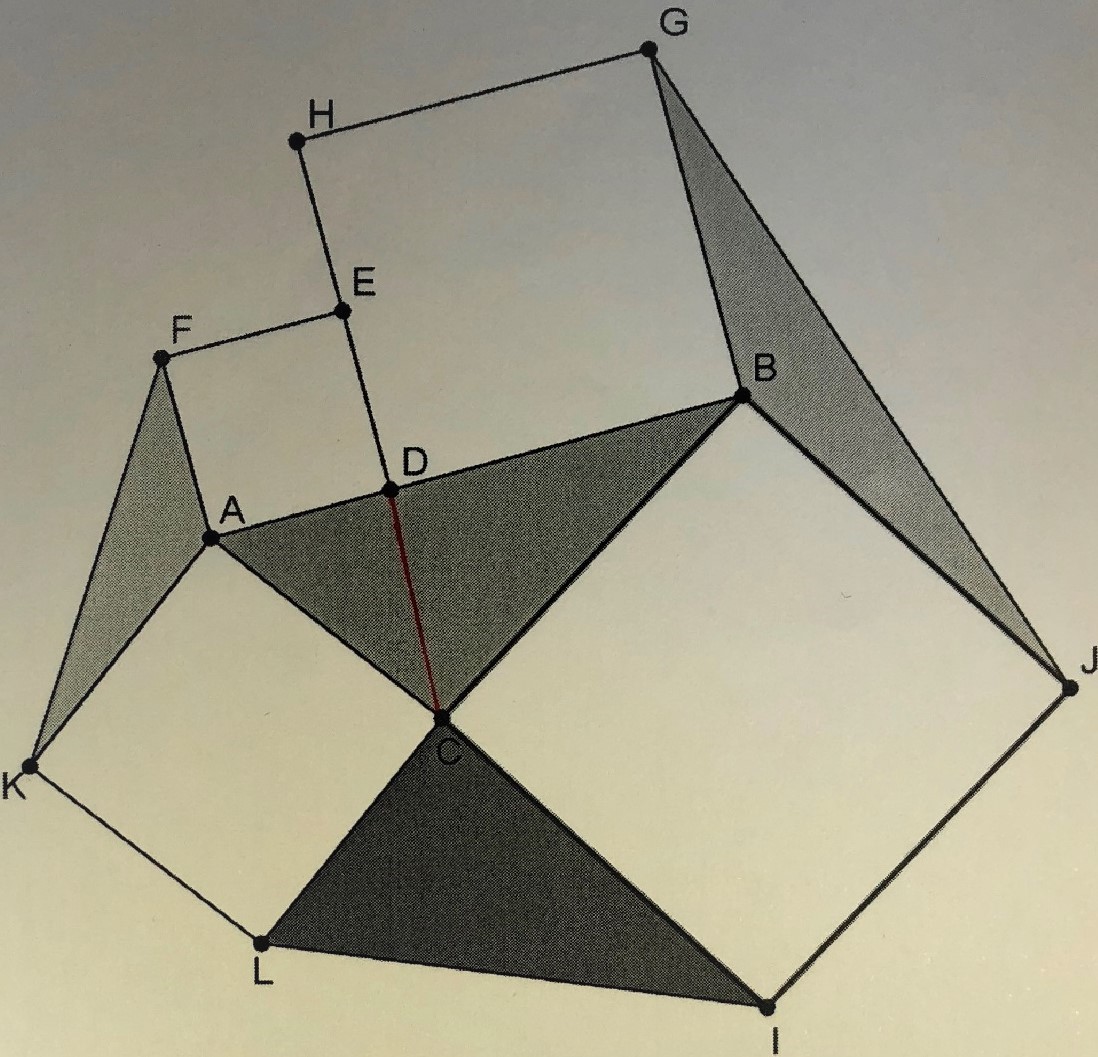
Triangle ABC = triangle CIL - as proven in part 1
Draw a line between C and D.
Triangle ACD = triangle AFK
Triangle BCD = triangle BGJ
Therefore, ABC = AFK + BGJ
Therefore, CIL = AFK + BGJ
Surprising Equalities
Age 14 to 18
Challenge Level 
Mathula from Doha College in Qatar made some observations using GeoGebra. Mathula's work below includes finding the areas manually using the cosine rule
($a^2 = b^2 + c^2 - 2bc\cos A$) and the formula for the area of a triangle $A=\frac12 ab\sin C$.
Beste and YiÄŸit from Amasya Åžehit Ferhat Ãœnelli Bilim Ve Sanat Merkezi in Turkey, Max, Ashwin, Jayden and Will and Jakob and Scott from Abingdon School in the UK and Mathula all proved that the four triangles have the same area using these two rules. This is Jakob and Scott's work:
This is Mathula's explanation of step 5:
The sine wave has an axis of symmetry at 90, as $\sin{0}$ and $\sin{180}$ have the same value.
The red text says:
these points are equidistant from the line of symmetry, which means they are equidistant from $0$ and $180$
if one of these points is $x$, the other point is $(90-x)+90=180-x$ AND THEY HAVE THE SAME $\sin x$ VALUE
There is another method which the second interactivity in the Getting Started section can help you find.
Click to see the solution using this method.
The areas of each of the four triangles are the same. We can show this for triangles $ABC$ and $ADE$ by rotating the triangle $ADE$ through $90^{\circ}$ anticlockwise, so that $AD$ lies along $AC$ (the blue shaded triangle). Then $AB=AE'$, so $AC$ is a median of the triangle $BCE'$. Hence triangle $ABC$ has the same area as triangle $ACE'$ and therefore also the triangle $ADE$. (Or we can just notice that $BA=AE'$ and triangles $ABC$ and $ACE'$ have the same perpendicular height).
Beste and YiÄŸit, Max, Ashwin, Jayden and Will and Mathula used their result about the triangle to prove similar results about the quadrilateral and the triangle with two squares on one side. This is Beste and YiÄŸit's work on the quadrilateral:
This Max, Ashwin, Jayden and Will's work on the triangle with two squares on one side, with Beste and YiÄŸit's diagram.
Triangle ABC = triangle CIL - as proven in part 1
Draw a line between C and D.
Triangle ACD = triangle AFK
Triangle BCD = triangle BGJ
Therefore, ABC = AFK + BGJ
Therefore, CIL = AFK + BGJ
You may also like
Just Rolling Round
P is a point on the circumference of a circle radius r which rolls, without slipping, inside a circle of radius 2r. What is the locus of P?
30-60-90 Polypuzzle
Re-arrange the pieces of the puzzle to form a rectangle and then to form an equilateral triangle. Calculate the angles and lengths.