Skip over navigation
As well as the proof suggested in the hint, it is possible to prove the result using trigonometric formulae, so the problem is a great opportunity to consolidate work on different areas of the geometry curriculum as well as appreciating the elegance of a variety of solution methods.
Students could begin by drawing triangles on dotty paper and then constructing the squares on the sides like those created in Tilted Squares. Then they could work out the areas of the triangles using Pick's Theorem. They may then wish to move on to using GeoGebra to see if any relationships they notice still hold for the many cases they can generate dynamically.
The article Using Digital Manipulatives and Interactivities to Develop Curiosity emphasises the importance of proof when using dynamic geometry; students should not be satisfied by seeing the areas stay the same in the software, as there could be rounding errors. We can't be sure that the areas are always equal unless we prove it!
In the Getting Started section, there is an interactive GeoGebra applet which shows the outer triangles rotating to line up with the original triangle. This, together with the diagram in the problem and the supporting questions, can be used to help students work towards a proof. Alternatively, students who have met the formula $\frac12ab \sin C$ for the area of a triangle could be encouraged to use this, together with their understanding of the relationship between $\sin \theta$ and $\sin (180-\theta)$, to construct a proof.
The two follow-up problems offer a good opportunity for students to adapt their thinking from the first part of the problem and apply it to a new situation.
If I knew the sides and the angles, how would I work out the area of the triangle?
How are the angles of the original triangle and the new triangles related?

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Surprising Equalities
Age 14 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Why do this problem?
This problem presents students with a surprising result which we hope they will want to explain. By using dynamic geometry, students can see that the triangles appear to have the same area regardless of the starting configuration, but to provide a convincing explanation and proof will require some determination and resilience.As well as the proof suggested in the hint, it is possible to prove the result using trigonometric formulae, so the problem is a great opportunity to consolidate work on different areas of the geometry curriculum as well as appreciating the elegance of a variety of solution methods.
Possible approach
Students could begin by drawing triangles on dotty paper and then constructing the squares on the sides like those created in Tilted Squares. Then they could work out the areas of the triangles using Pick's Theorem. They may then wish to move on to using GeoGebra to see if any relationships they notice still hold for the many cases they can generate dynamically.
The article Using Digital Manipulatives and Interactivities to Develop Curiosity emphasises the importance of proof when using dynamic geometry; students should not be satisfied by seeing the areas stay the same in the software, as there could be rounding errors. We can't be sure that the areas are always equal unless we prove it!
In the Getting Started section, there is an interactive GeoGebra applet which shows the outer triangles rotating to line up with the original triangle. This, together with the diagram in the problem and the supporting questions, can be used to help students work towards a proof. Alternatively, students who have met the formula $\frac12ab \sin C$ for the area of a triangle could be encouraged to use this, together with their understanding of the relationship between $\sin \theta$ and $\sin (180-\theta)$, to construct a proof.
The two follow-up problems offer a good opportunity for students to adapt their thinking from the first part of the problem and apply it to a new situation.
Key questions
Does it help to add any new lines, or to rotate part of the diagram?If I knew the sides and the angles, how would I work out the area of the triangle?
How are the angles of the original triangle and the new triangles related?
Possible extension
Students could try Areas and Ratios, which explores idea of areas of triangles with a shared vertex further.Possible support
Triangle in a Triangle might provide a useful warm-up to get students thinking about methods of geometrical proof.You may also like
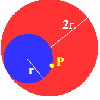
Just Rolling Round
P is a point on the circumference of a circle radius r which rolls, without slipping, inside a circle of radius 2r. What is the locus of P?
30-60-90 Polypuzzle
Re-arrange the pieces of the puzzle to form a rectangle and then to form an equilateral triangle. Calculate the angles and lengths.

