Skip over navigation
Demirhan from Dubai British School has made a good start on this investigation by finding formulae for the side lengths of the Nth triangle in the spiral:
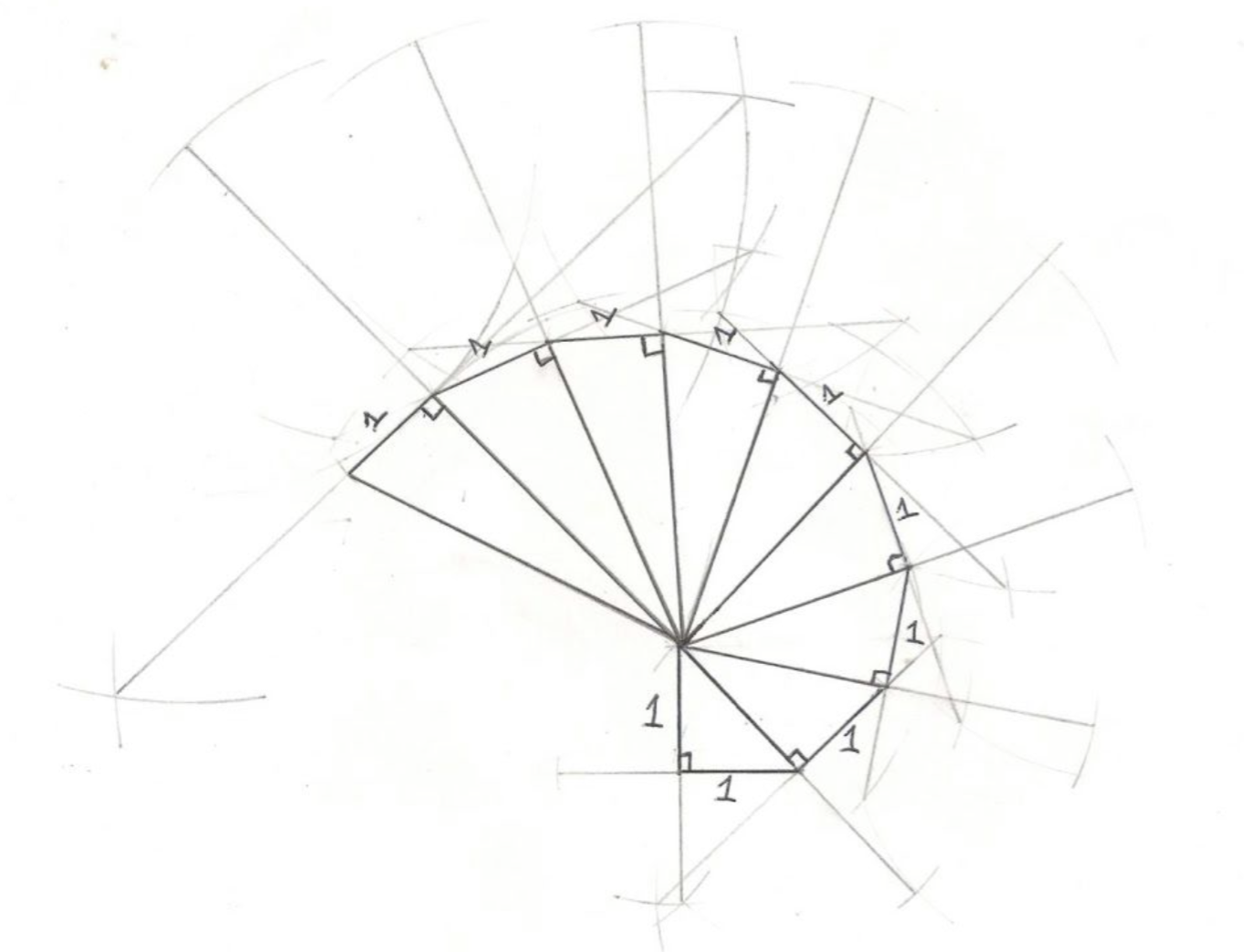
In the irrational construction problem I took into fact that the bottom side of the triangle will always be 1cm as shown in the picture. While the other side which isn't the hypotenuse on the first triangle was 1cm. Using the Pythagoras theorem ($A^2+B^2=C^2$) I figured out the first hypotenuse of the triangle as $\sqrt{1+1}$, which is $\sqrt{2}$. The hypotenuse of one triangle is the same as the non-hypotenuse side of the triangle after it. So the hypotenuse of the second triangle is going to be $\sqrt{2+1} = \sqrt{3}$. So the hypotenuse of the third triangle is going to be $\sqrt{3+1}=\sqrt{4}$.
In general, If $N$ is the number for the consecutive triangle then:
The Hypotenuse of the triangle will be $\sqrt{N+1}$
So this shows we can find any length of the form $\sqrt{N}$ in the diagram!
Sergio from Kings College of Alicante has suggested another way to construct $\sqrt{13}$
If 13 is the hypotenuse of the triangle and a,b are the two sides, following pythagoras theory then $a$ squared plus $b$ square must add up to to 13. I looked at sqaure numbers and I simply figured which number a and b had to be in seconds: $a=2$ and $b=3$.
Pablo from Kings College of Alicante has found a way to construct this diagram exactly using only a straight-edge and compass, which is explained here.
Irrational Constructions
Age 16 to 18
Challenge Level 
Demirhan from Dubai British School has made a good start on this investigation by finding formulae for the side lengths of the Nth triangle in the spiral:
In the irrational construction problem I took into fact that the bottom side of the triangle will always be 1cm as shown in the picture. While the other side which isn't the hypotenuse on the first triangle was 1cm. Using the Pythagoras theorem ($A^2+B^2=C^2$) I figured out the first hypotenuse of the triangle as $\sqrt{1+1}$, which is $\sqrt{2}$. The hypotenuse of one triangle is the same as the non-hypotenuse side of the triangle after it. So the hypotenuse of the second triangle is going to be $\sqrt{2+1} = \sqrt{3}$. So the hypotenuse of the third triangle is going to be $\sqrt{3+1}=\sqrt{4}$.
In general, If $N$ is the number for the consecutive triangle then:
The Hypotenuse of the triangle will be $\sqrt{N+1}$
So this shows we can find any length of the form $\sqrt{N}$ in the diagram!
Sergio from Kings College of Alicante has suggested another way to construct $\sqrt{13}$
If 13 is the hypotenuse of the triangle and a,b are the two sides, following pythagoras theory then $a$ squared plus $b$ square must add up to to 13. I looked at sqaure numbers and I simply figured which number a and b had to be in seconds: $a=2$ and $b=3$.
Pablo from Kings College of Alicante has found a way to construct this diagram exactly using only a straight-edge and compass, which is explained here.
You may also like
Powerful Quadratics
This comes in two parts, with the first being less fiendish than the second. It’s great for practising both quadratics and laws of indices, and you can get a lot from making sure that you find all the solutions. For a real challenge (requiring a bit more knowledge), you could consider finding the complex solutions.
Discriminating
You're invited to decide whether statements about the number of solutions of a quadratic equation are always, sometimes or never true.
Factorisable Quadratics
This will encourage you to think about whether all quadratics can be factorised and to develop a better understanding of the effect that changing the coefficients has on the factorised form.