Skip over navigation
Thank you to Sophie, Mimi, Hannah and Emma from Sandbach High School who submitted the answers to this problem in the diagrams below:
Thank you also to Melissa who has given explanations for how she arrived at her answers:
First part:
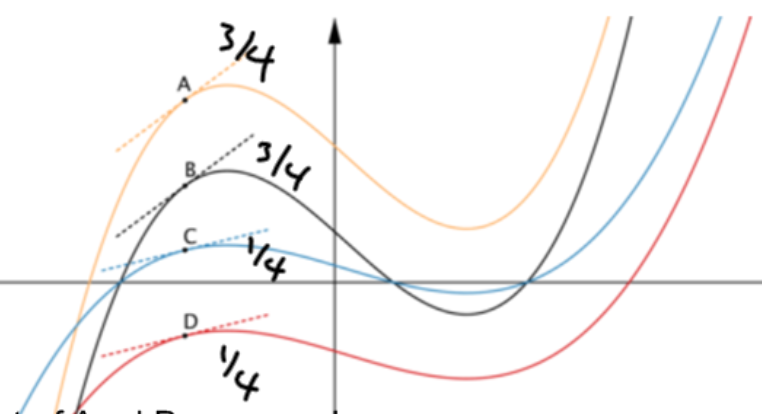
The graphs are all transformations of $y = f(x)$ so $y = 3 f(x)$ and $y = 3f(x) + 8$ can be easily spotted as the lines with steeper gradients, with $y = 3f(x) + 8$ being higher up on the graph. Similarly, of $y = f(x)$ and $y = f(x) - 8$, $y = f(x) - 8$ is the line which is seen to be lower down on the graph. So the yellow, black, blue and red lines show $y = 3f(x) + 8$, $y = 3f(x)$, $y = f(x)$ and $y = f(x) - 8$ respectively.
A and B will have gradients three times as large as the gradients of C and D because for each increase by one in the x value, 3f(x) increases by three times as much as f(x) does.
This means that when the gradient of D is $\frac{1}{4}$, the gradient of C is also $\frac{1}{4}$ and the gradients of A and B are $3\times\frac{1}{4} = \frac{3}{4}$.
Second part:
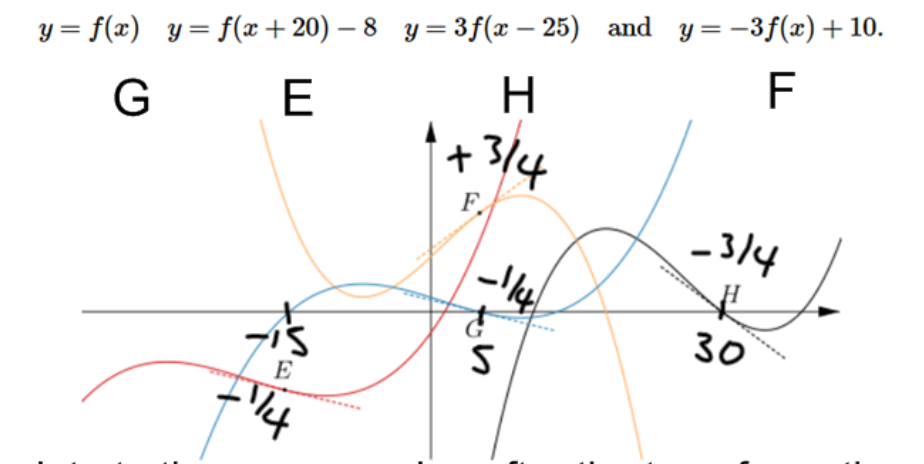
The yellow line has been reflected in the x axis compared with the others because it starts off decreasing whereas the others begin increasing. Therefore the yellow line is $y = -3f(x) + 10$.
The black line has the same gradient as the yellow line, which is a steeper gradient than the others so the black shows $y = 3f(x - 25)$.
The red line is further left than the blue line so the red line shows $y = f(x + 20)-8$ and the blue line shows $y = f(x)$.
The points E, F, G and H are the same point translated from the original curve, which can easily be seen by looking at how far horizontally and vertically the points E, F and G have been translated from H.
The gradient at E is $-\frac{1}{4}$ so the gradient at G is also $-\frac{1}{4}$ because $y = f(x + 20)$ has the same shape as $y = f(x)$, it is translated but not stretched. The gradient at H is $-\frac{3}{4}$ because the graph $y = 3f(x - 25)$ has been stretched along the y axis by a scale factor of 3 from $y = f(x)$ so the gradient is three times that of G. The gradient at F is $\frac{3}{4}$ because the gradient is the same as at H but is positive.



Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Slippery Slopes
Age 16 to 18
Challenge Level 





- Problem
- Student Solutions
Thank you to Sophie, Mimi, Hannah and Emma from Sandbach High School who submitted the answers to this problem in the diagrams below:


Thank you also to Melissa who has given explanations for how she arrived at her answers:
First part:
The graphs are all transformations of $y = f(x)$ so $y = 3 f(x)$ and $y = 3f(x) + 8$ can be easily spotted as the lines with steeper gradients, with $y = 3f(x) + 8$ being higher up on the graph. Similarly, of $y = f(x)$ and $y = f(x) - 8$, $y = f(x) - 8$ is the line which is seen to be lower down on the graph. So the yellow, black, blue and red lines show $y = 3f(x) + 8$, $y = 3f(x)$, $y = f(x)$ and $y = f(x) - 8$ respectively.
A and B will have gradients three times as large as the gradients of C and D because for each increase by one in the x value, 3f(x) increases by three times as much as f(x) does.
This means that when the gradient of D is $\frac{1}{4}$, the gradient of C is also $\frac{1}{4}$ and the gradients of A and B are $3\times\frac{1}{4} = \frac{3}{4}$.
Second part:
The yellow line has been reflected in the x axis compared with the others because it starts off decreasing whereas the others begin increasing. Therefore the yellow line is $y = -3f(x) + 10$.
The black line has the same gradient as the yellow line, which is a steeper gradient than the others so the black shows $y = 3f(x - 25)$.
The red line is further left than the blue line so the red line shows $y = f(x + 20)-8$ and the blue line shows $y = f(x)$.
The points E, F, G and H are the same point translated from the original curve, which can easily be seen by looking at how far horizontally and vertically the points E, F and G have been translated from H.
The gradient at E is $-\frac{1}{4}$ so the gradient at G is also $-\frac{1}{4}$ because $y = f(x + 20)$ has the same shape as $y = f(x)$, it is translated but not stretched. The gradient at H is $-\frac{3}{4}$ because the graph $y = 3f(x - 25)$ has been stretched along the y axis by a scale factor of 3 from $y = f(x)$ so the gradient is three times that of G. The gradient at F is $\frac{3}{4}$ because the gradient is the same as at H but is positive.
You may also like
Powerful Quadratics
This comes in two parts, with the first being less fiendish than the second. It’s great for practising both quadratics and laws of indices, and you can get a lot from making sure that you find all the solutions. For a real challenge (requiring a bit more knowledge), you could consider finding the complex solutions.
Discriminating
You're invited to decide whether statements about the number of solutions of a quadratic equation are always, sometimes or never true.
Factorisable Quadratics
This will encourage you to think about whether all quadratics can be factorised and to develop a better understanding of the effect that changing the coefficients has on the factorised form.

