Skip over navigation
To get you started, the diagrams below record a potential route through each of the problems.
The numbers record the order in which the different cells could be filled in on the grids.
Of course, there are other possible routes through the problems.
The places where the number is in brackets indicates that there is a choice of number that can be placed there.
1.
The number that you can work out is the product of the numbers in that column. The other column products might help you work this out.
4.
One possibility is to consider first where the number 9 might go, looking at all the rows and columns.
You might then want to consider where the number 16 might go. Thinking about the row DEF and the column CFI in particular might be useful here in narrowing down the options.
After that, try to see how much of the grid each combination lets you fill in!
Gabriel's Problem
Age 11 to 14
Challenge Level 
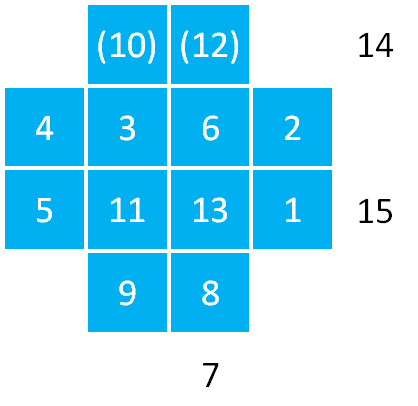
To get you started, the diagrams below record a potential route through each of the problems.
The numbers record the order in which the different cells could be filled in on the grids.
Of course, there are other possible routes through the problems.
The places where the number is in brackets indicates that there is a choice of number that can be placed there.
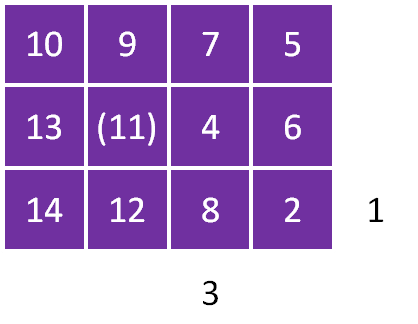
1.
2.
3.
What do you think that the number outside the grid might indicate?
The number that you can work out is the product of the numbers in that column. The other column products might help you work this out.
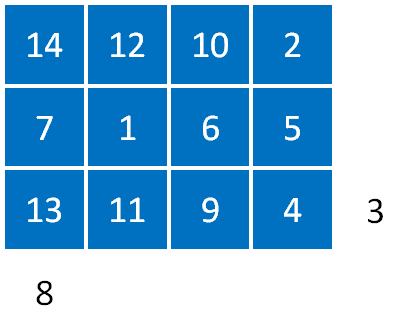
4.
5.
6.
7.
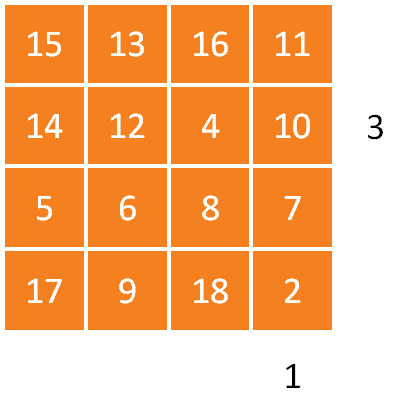
8. There are a number of different routes through this problem, depending on what you do.
One possibility is to consider first where the number 9 might go, looking at all the rows and columns.
You might then want to consider where the number 16 might go. Thinking about the row DEF and the column CFI in particular might be useful here in narrowing down the options.
After that, try to see how much of the grid each combination lets you fill in!
Related Collections
You may also like
Adding All Nine
Make a set of numbers that use all the digits from 1 to 9, once and once only. Add them up. The result is divisible by 9. Add each of the digits in the new number. What is their sum? Now try some other possibilities for yourself!
