The Farmers' Field Boundary

The Farmers' Field Boundary printable sheet

Two farmers each have a field with a shared boundary. On the boundary is a tap. 

The farmers decide it would be more convenient if the boundary was a straight line, but they both need to access the tap.

Your challenge is to redraw the boundary so that:

• Both farmers can access the tap
• The boundary line is straight
• The new fields have the same areas as the original fields

You can use the interactivity below to explore this problem with a variety of fields.
Move the points to create two fields, then click Fix Fields.

Once you have created your fields, a purple dot will appear which you can move to create the new field boundary.
When you think your new fields have the same area as the original fields, you can tick the "Show areas" box to see how close you are.

Can you come up with a geometrical method for constructing the position of the new boundary?

Can you adapt your method to construct a boundary for a more complicated situation like the one pictured below?
 

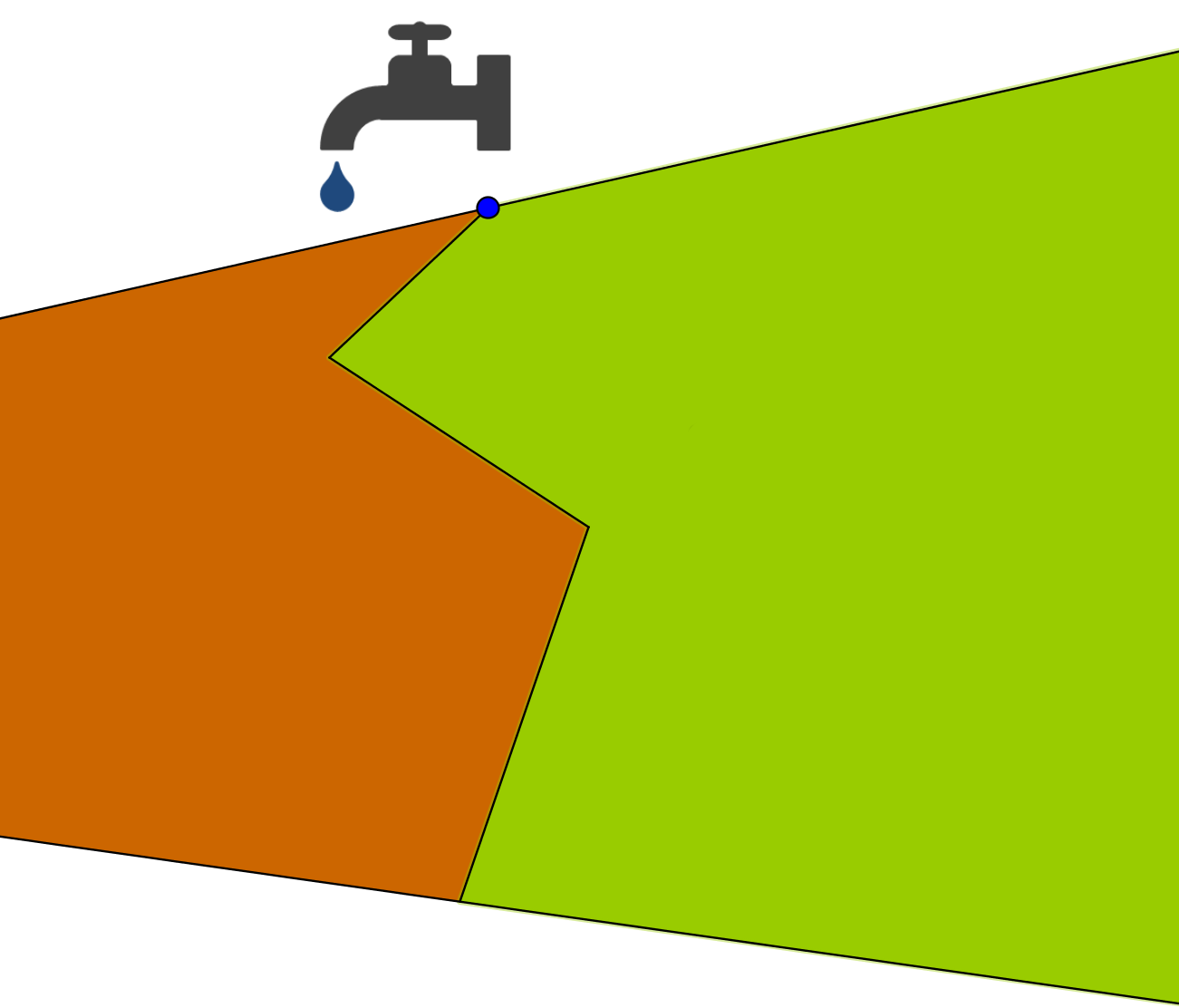
Can you describe a method for redrawing boundaries with four, five, or more straight lines into a single straight line?