The Farmers' Field Boundary

This was a fascinating problem which included an interactive feature to help you explore your ideas.

Let's begin by looking at the first part of the problem. You needed to use the interactivity to create two fields which shared the tap at A and maintained the same areas.

Here's a screenshot of a solution sent in by from Shriram, from India:

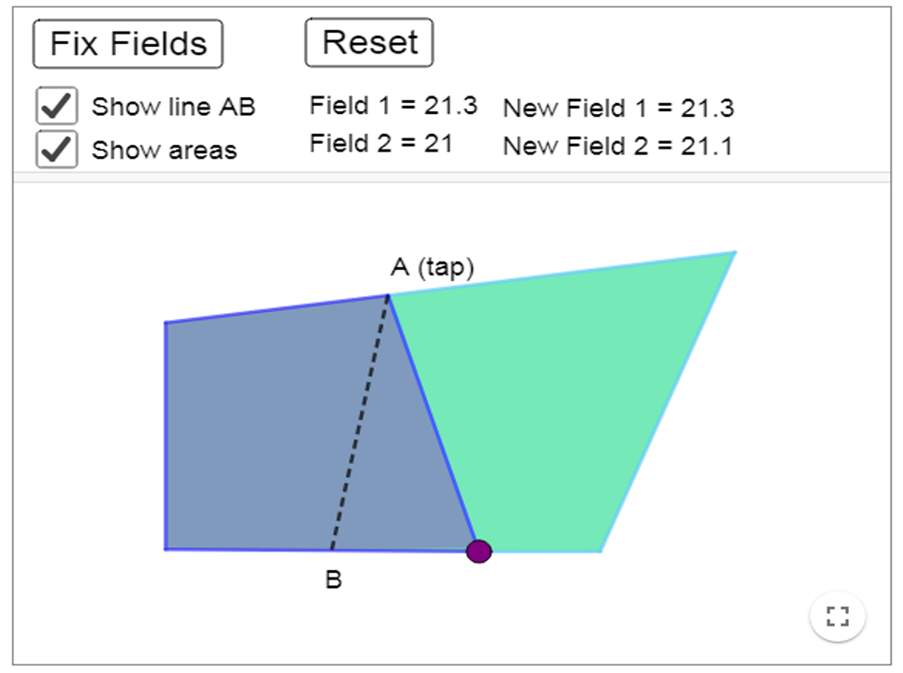
Zavya, Miraya and Methuli from Heckmondwike Grammar School in Engliand also sent in screenshots. This is one of Zavya's screenshots:

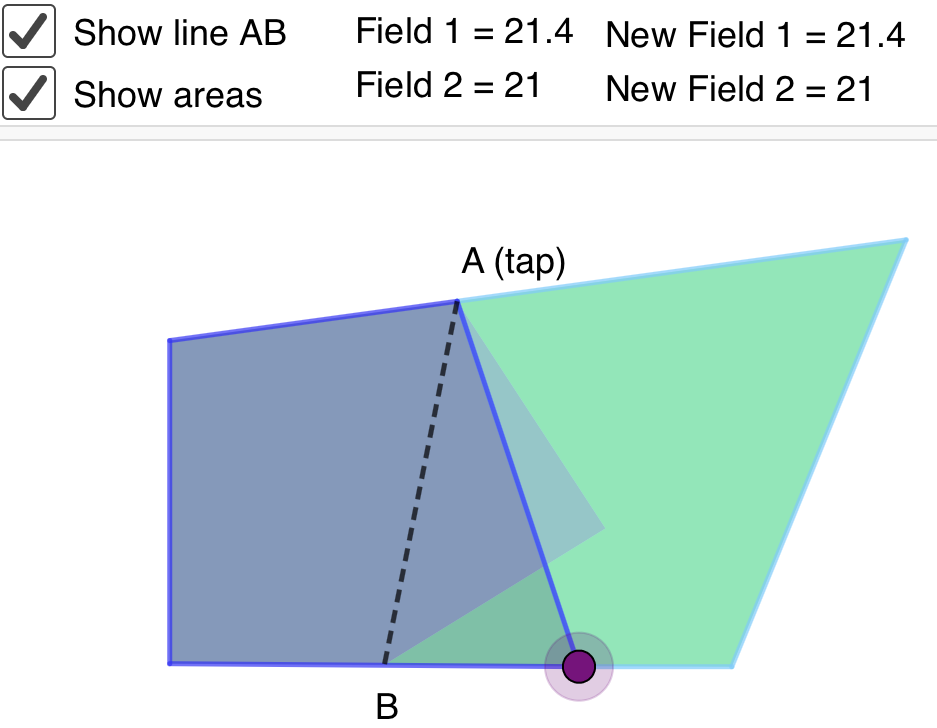
This is one of Methuli's screenshots:

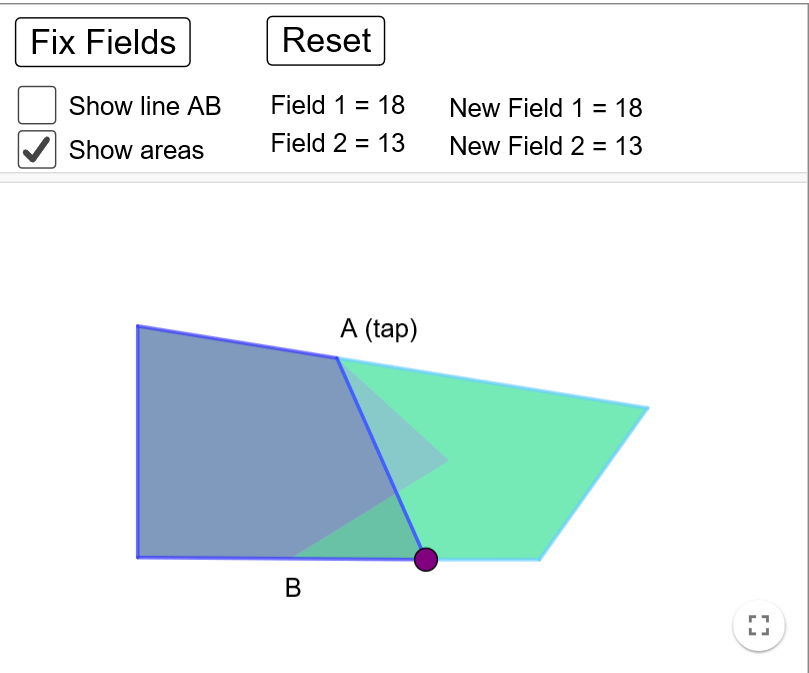
Miranda sent in some correct solutions drawn by hand but didn't explain her method:

Kirsty from Lancing College and David from the UK explained how to form the correct boundary. Here is David's work:

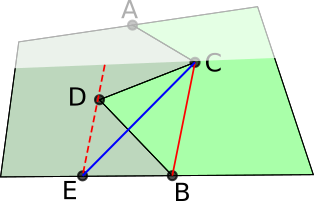
 Construct the line parallel to AB through C. We claim that triangle ABB' has the same area as triangle ABC.

If they do have the same area, then line AB' is the new boudary. This is because changing from ACB to AB, the farmer on the left loses triangle ABC. Then changing the boundary from AB to AB', the farmer on the left gains ABB'.

Clearly, they both share the same base AB. Furthermore, as AB is parallel to CB' (by construction), the area of triangle ABB' is the same as the area of triangle ABC. This is because a triangle's area can be determined solely from $0.5\times\text{base}\times\text{perpendicular height},$ and the two perpendicular heights in this case are the perpendicular distances between two parallel lines (which are constant). So AB' is the required straight line.

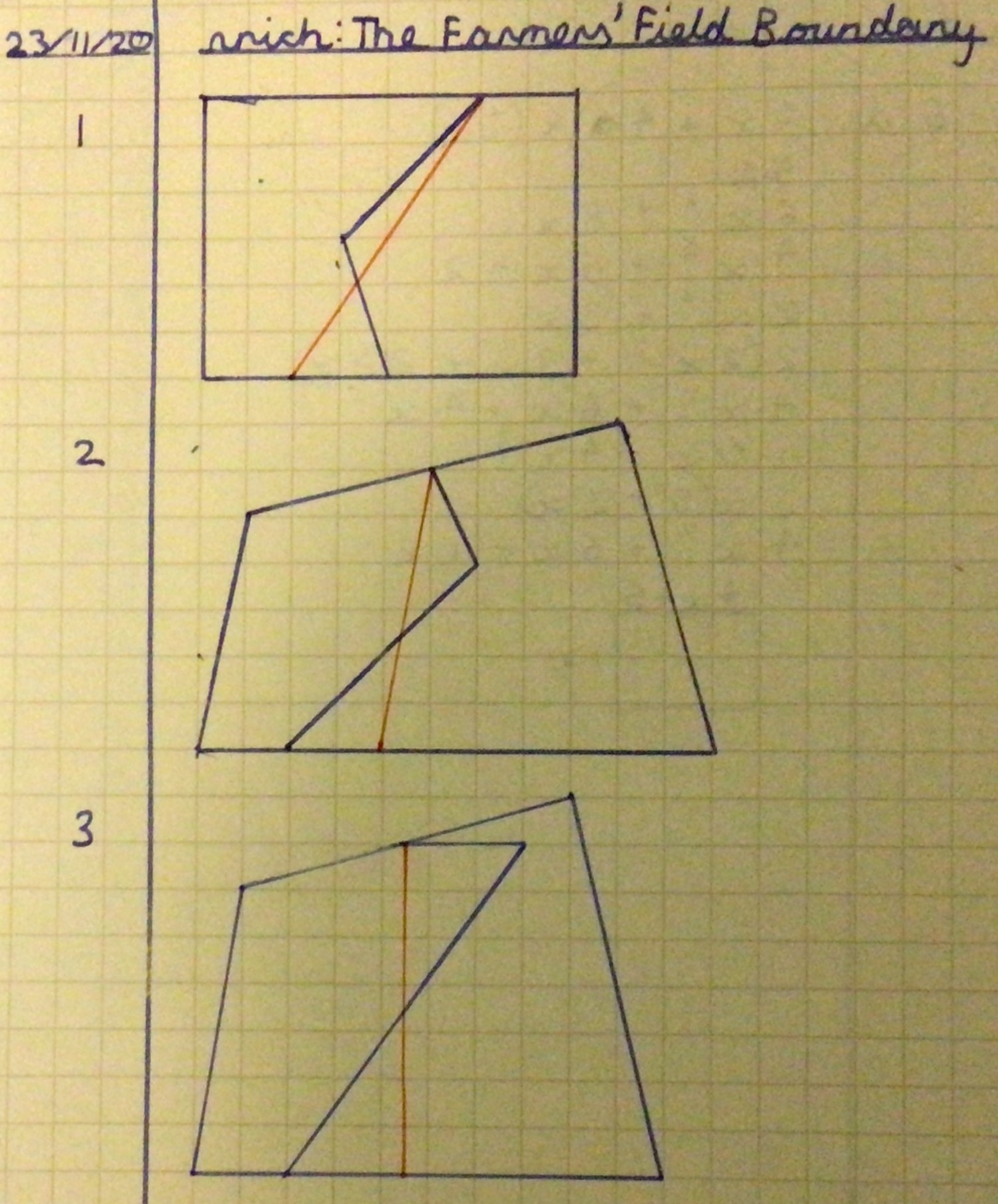
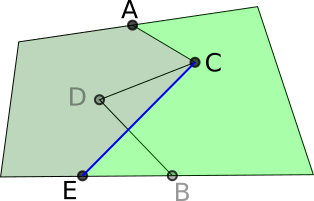
Kirsty extended this idea to fields with more complicated boundaries. Here is Kirsty's work with a couple of extra diagrams added: