Skip over navigation
Geometry sometimes offers surprising results that can be proved very elegantly. This is a great example of how finding the right representation (in this case a diagram) allows a problem to be solved more easily.
Show students the image:
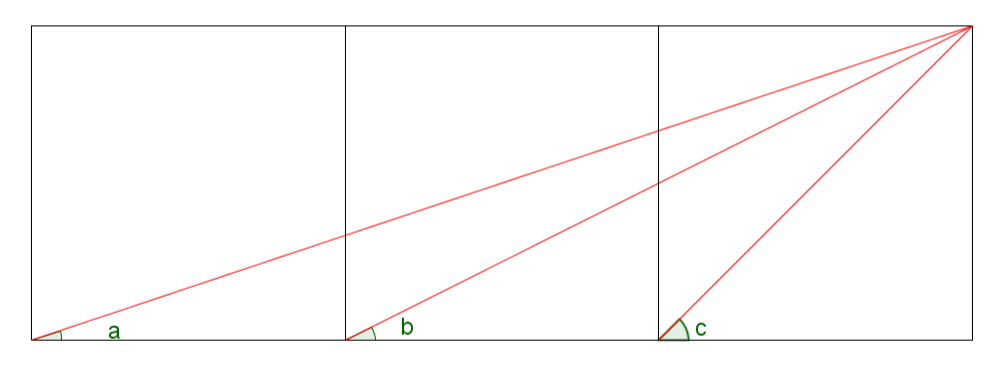
Invite them to draw it and measure angles a, b and c to verify that a+b=c, and give them some time to think about how they might prove it. There are many methods that use advanced techniques such as trigonometry or vectors, but there is also an elegant geometric method. Once they have had time to engage with the difficulty of the problem, show them the following image:
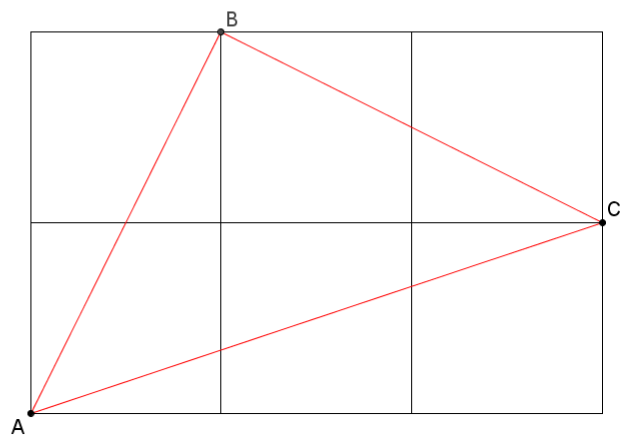
"Can you find angles in the diagram that are the same size as angles a and b?"
"What can you say about the angle at B?"
"What can you say about the lengths AB and BC?"
"What can you deduce about the angles at A and C?"
Students may be interested to read 8 Methods for Three by One which outlines a number of different methods for this proof using more advanced mathematics.
Angles in Polygons Short Problems worksheets offer some more straightforward examples of geometrical reasoning problems.

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Angles in Three Squares
Age 14 to 16
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Why do this problem?
Geometry sometimes offers surprising results that can be proved very elegantly. This is a great example of how finding the right representation (in this case a diagram) allows a problem to be solved more easily.
Possible approach
Show students the image:
Invite them to draw it and measure angles a, b and c to verify that a+b=c, and give them some time to think about how they might prove it. There are many methods that use advanced techniques such as trigonometry or vectors, but there is also an elegant geometric method. Once they have had time to engage with the difficulty of the problem, show them the following image:

"Can you find angles in the diagram that are the same size as angles a and b?"
"What can you say about the angle at B?"
"What can you say about the lengths AB and BC?"
"What can you deduce about the angles at A and C?"
Possible extension
Students may be interested to read 8 Methods for Three by One which outlines a number of different methods for this proof using more advanced mathematics.
Possible support
Angles in Polygons Short Problems worksheets offer some more straightforward examples of geometrical reasoning problems.You may also like
At a Glance
The area of a regular pentagon looks about twice as a big as the pentangle star drawn within it. Is it?
No Right Angle Here
Prove that the internal angle bisectors of a triangle will never be perpendicular to each other.

