Skip over navigation
Well done to Vid from Osnovna Å¡ola Loka ÄŒrnomelj in Slovenia, who sent us the following solution to the problem:
Angle $c = 45^\circ$ because it is the angle between the diagonal and the side of a square. To prove that $a+b=c$, I shall begin by adding points to the diagram to help with naming angles:
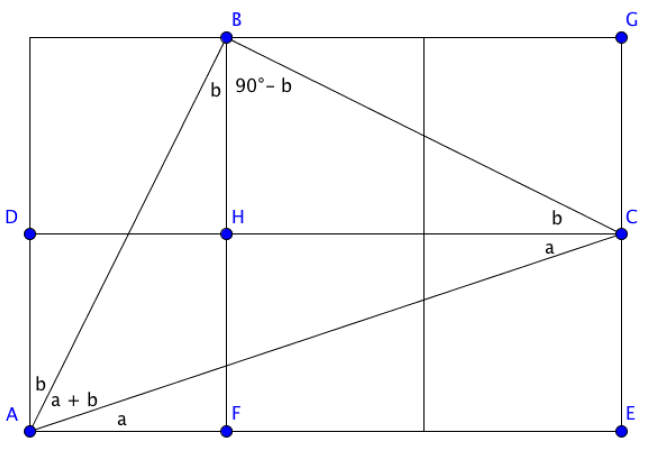
Now we can find several angles:
Therefore, adding the angles of $\triangle ABC$ together, we have: $$\begin{align}\angle ABC + \angle BAC + \angle ACB &= 180^\circ \\
((90^\circ - b) + b) + (a + b) + (a + b) &= 180^\circ \\
90^\circ + (a + b) + (a + b) &= 180^\circ\\
90^\circ + 2(a + b) &= 180^\circ\\
2(a + b) &= 180^\circ - 90^\circ\\
2(a + b) &= 90^\circ\\
a + b &= \frac{90^\circ}{2}\\
a + b &= 45^\circ\end{align}$$
Therefore, since $c = 45^\circ$, we have that $a + b = c$.

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Angles in Three Squares
Age 14 to 16
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Well done to Vid from Osnovna Å¡ola Loka ÄŒrnomelj in Slovenia, who sent us the following solution to the problem:
Angle $c = 45^\circ$ because it is the angle between the diagonal and the side of a square. To prove that $a+b=c$, I shall begin by adding points to the diagram to help with naming angles:

Now we can find several angles:
- Firstly, $\angle CAE = a$ and $\angle BAD = b$.
- Since $DC$ is parallel to $AE$, by alternate angles, we know that $\angle DCA = \angle CAE$.
- Next, we can see that $\angle BCD = b$.
- Similarly, $\angle ABF = \angle CBG = b$.
- Since $\angle BHC$ is a right angle and the sum of angles in a triangle is $180^\circ$, then we have that $\angle CBH = 180^\circ - 90^\circ - b = 90^\circ - b$.
- Hence, we have that $\angle BCA = a + b$.
- In $\triangle ABC$, the line segments $AB$ and $BC$ have equal length, so we have that $\triangle ABC$ is isosceles. Therefore, $\angle BAC = \angle BCA = a+b$.
Therefore, adding the angles of $\triangle ABC$ together, we have: $$\begin{align}\angle ABC + \angle BAC + \angle ACB &= 180^\circ \\
((90^\circ - b) + b) + (a + b) + (a + b) &= 180^\circ \\
90^\circ + (a + b) + (a + b) &= 180^\circ\\
90^\circ + 2(a + b) &= 180^\circ\\
2(a + b) &= 180^\circ - 90^\circ\\
2(a + b) &= 90^\circ\\
a + b &= \frac{90^\circ}{2}\\
a + b &= 45^\circ\end{align}$$
Therefore, since $c = 45^\circ$, we have that $a + b = c$.
You may also like
At a Glance
The area of a regular pentagon looks about twice as a big as the pentangle star drawn within it. Is it?
No Right Angle Here
Prove that the internal angle bisectors of a triangle will never be perpendicular to each other.

