Isometric Areas
Let's define a unit of area, $T$, such that the triangle has area $1T$.
Here are some parallelograms whose side lengths are whole numbers.
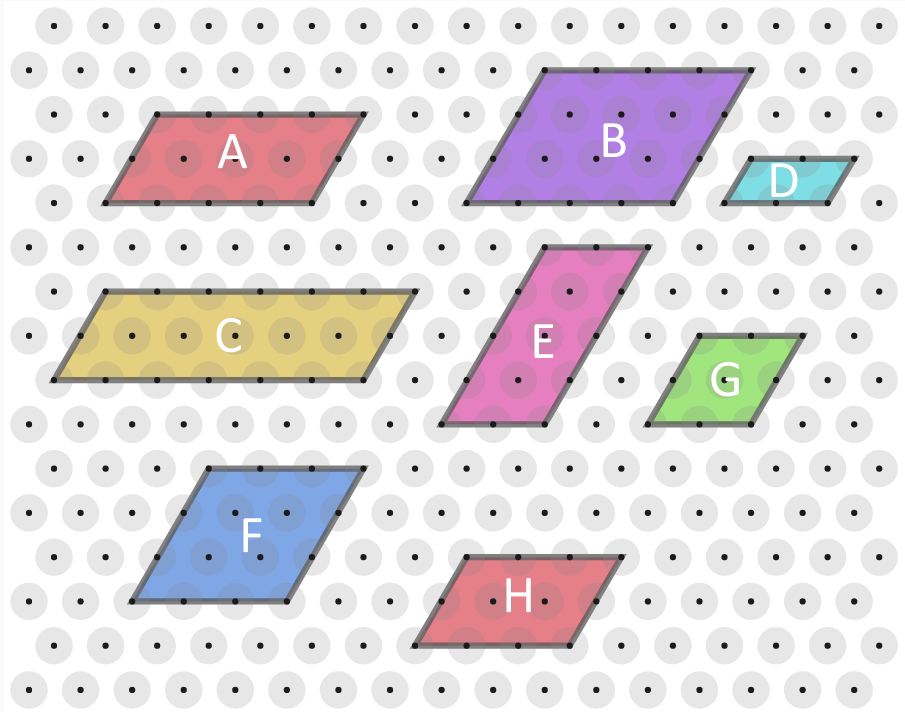
Can you find the area, in terms of $T$, of each parallelogram?
Compare the results with the lengths of their edges.
What do you notice?
Can you explain what you've noticed?
Can you find a similar result for trapeziums in which all four lengths are whole numbers?
You might like to try More Isometric Areas next.
You may also like
Isosceles
Prove that a triangle with sides of length 5, 5 and 6 has the same area as a triangle with sides of length 5, 5 and 8. Find other pairs of non-congruent isosceles triangles which have equal areas.
Linkage
Four rods, two of length a and two of length b, are linked to form a kite. The linkage is moveable so that the angles change. What is the maximum area of the kite?