Skip over navigation
Well done to Jessica from Tiffin Girls' School and Minhaj from St Ivo School who both found proofs of the two identities using these diagrams.
Jessica's idea, for both identities, was to use the two right angled triangles $\triangle AOB$ and $\triangle ACB$ in the diagram below.
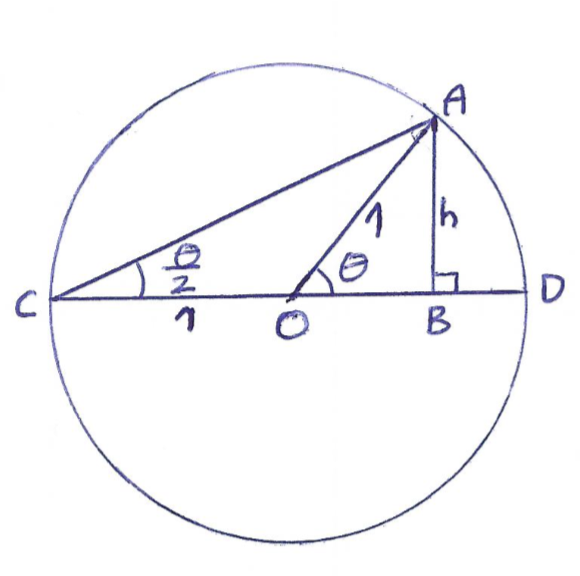
To prove $\cos^2{\frac{\theta}{2}} \equiv \frac{1}{2}(1+\cos{\theta})$
In $\triangle AOB$:
$OB=\sqrt{1-h^2}$ (by using Pythagoras' Theorem)
$\cos{\theta}=\frac{OB}{OA} =\sqrt{1-h^2}$
$h^2=1-\cos^2{\theta}$
In $\triangle ACB$:
$BC=BO+OC=1+\sqrt{1-h^2}$
$AC^2=AB^2+BC^2=h^2+(1+\sqrt{1-h^2})^2$
$\cos^2{\frac{\theta}{2}}=\frac{BC^2}{AC^2}=\frac{(1+\sqrt{1-h^2})^2}{(1+\sqrt{1-h^2})^2+h^2}$
Since we know $\cos{\theta}=\sqrt{1-h^2}$ and $h^2=1-\cos^2{\theta}$ we can get this in terms of $\cos{\theta}$:
$\cos^2{\frac{\theta}{2}}=\frac{(1+\cos{\theta})^2}{(1+\cos{\theta})^2+1-\cos^2{\theta}}=\frac{(1+\cos{\theta})^2}{2+2\cos{\theta}}=\frac{1}{2}(1+\cos{\theta})$
To prove $\sin^2{\frac{\theta}{2}} \equiv \frac{1}{2}(1-\cos{\theta})$:
In $\triangle AOB$:
$\sin{\theta}=\frac{AB}{AO}=\frac{h}{1}=h$
In $\triangle ACB$:
$\sin^2{\frac{\theta}{2}}=\frac{h^2}{(1+\sqrt{1-h^2})^2+h^2}$
As in the previous proof we can use $\cos{\theta}=\sqrt{1-h^2}$ and $h^2=1-\cos^2{\theta}$ to get:
$\sin^2{\frac{\theta}{2}}=\frac{1-\cos^2{\theta}}{(1+\cos{\theta})^2+1-\cos^2{\theta}}=\frac{(1+\cos{\theta})(1-\cos{\theta})}{2(1+\cos{\theta})}=\frac{1}{2}(1-\cos{\theta})$
Minhaj found an alternative way to prove these identies using different diagrams. Here is his proof of $\cos^2{\frac{\theta}{2}} \equiv \frac{1}{2}(1+\cos{\theta})$.
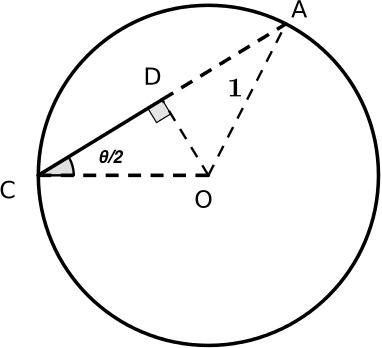
Note: In triangle AOC, lines CD and DA are equal (circle theorem: OD passes through the centre of the circle and is the perpendicular bisector of the chord CA, therefore since it bisects CA, CD=DA)
1. $\cos{\frac{\theta}{2}} = \frac{CD}{1}=CD$. Since $CD=DA$, $DA=\cos{\frac{\theta}{2}}$ too.
2. So $CA = CD + DA = 2 \cos{\frac{\theta}{2}}$
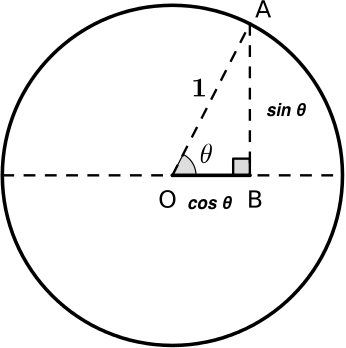
3. Have that $CB = \cos{\theta}+1$ and $AB = \sin{\theta}$
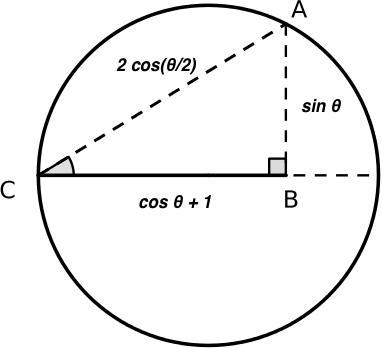
4. From Pythagoras' theorem have that $CB^2 + AB^2 = CA^2$,
so $(\cos{\theta}+1)^2 + \sin^2{\theta} = 4 \cos^2{\frac{\theta}{2}}$
5. Substituting $\sin^2{\theta} = 1-\cos^2{\theta}$ and rearranging gives:
$(\cos{\theta}+1)^2+(1-\cos^2{\theta}) = 4\cos^2{\frac{\theta}{2}}$
$cos^2{\theta}+2\cos{\theta}+1+1-\cos^2{\theta}=4\cos^2{\frac{\theta}{2}}$
$2 \cos{\theta}+2 = 4\cos^2{\frac{\theta}{2}}$
$\cos^2{\frac{\theta}{2}}=\frac{1}{2}(\cos{\theta}+1)$
Yet another way to complete this proof after point 3 without using pythagoras could be to look at the expression for $\cos{\frac{\theta}{2}}$ in the triangle $ACB$.



Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Proving Half-angle Formulae
Age 16 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
Well done to Jessica from Tiffin Girls' School and Minhaj from St Ivo School who both found proofs of the two identities using these diagrams.
Jessica's idea, for both identities, was to use the two right angled triangles $\triangle AOB$ and $\triangle ACB$ in the diagram below.

To prove $\cos^2{\frac{\theta}{2}} \equiv \frac{1}{2}(1+\cos{\theta})$
In $\triangle AOB$:
$OB=\sqrt{1-h^2}$ (by using Pythagoras' Theorem)
$\cos{\theta}=\frac{OB}{OA} =\sqrt{1-h^2}$
$h^2=1-\cos^2{\theta}$
In $\triangle ACB$:
$BC=BO+OC=1+\sqrt{1-h^2}$
$AC^2=AB^2+BC^2=h^2+(1+\sqrt{1-h^2})^2$
$\cos^2{\frac{\theta}{2}}=\frac{BC^2}{AC^2}=\frac{(1+\sqrt{1-h^2})^2}{(1+\sqrt{1-h^2})^2+h^2}$
Since we know $\cos{\theta}=\sqrt{1-h^2}$ and $h^2=1-\cos^2{\theta}$ we can get this in terms of $\cos{\theta}$:
$\cos^2{\frac{\theta}{2}}=\frac{(1+\cos{\theta})^2}{(1+\cos{\theta})^2+1-\cos^2{\theta}}=\frac{(1+\cos{\theta})^2}{2+2\cos{\theta}}=\frac{1}{2}(1+\cos{\theta})$
To prove $\sin^2{\frac{\theta}{2}} \equiv \frac{1}{2}(1-\cos{\theta})$:
In $\triangle AOB$:
$\sin{\theta}=\frac{AB}{AO}=\frac{h}{1}=h$
In $\triangle ACB$:
$\sin^2{\frac{\theta}{2}}=\frac{h^2}{(1+\sqrt{1-h^2})^2+h^2}$
As in the previous proof we can use $\cos{\theta}=\sqrt{1-h^2}$ and $h^2=1-\cos^2{\theta}$ to get:
$\sin^2{\frac{\theta}{2}}=\frac{1-\cos^2{\theta}}{(1+\cos{\theta})^2+1-\cos^2{\theta}}=\frac{(1+\cos{\theta})(1-\cos{\theta})}{2(1+\cos{\theta})}=\frac{1}{2}(1-\cos{\theta})$
Minhaj found an alternative way to prove these identies using different diagrams. Here is his proof of $\cos^2{\frac{\theta}{2}} \equiv \frac{1}{2}(1+\cos{\theta})$.

Note: In triangle AOC, lines CD and DA are equal (circle theorem: OD passes through the centre of the circle and is the perpendicular bisector of the chord CA, therefore since it bisects CA, CD=DA)
1. $\cos{\frac{\theta}{2}} = \frac{CD}{1}=CD$. Since $CD=DA$, $DA=\cos{\frac{\theta}{2}}$ too.
2. So $CA = CD + DA = 2 \cos{\frac{\theta}{2}}$

3. Have that $CB = \cos{\theta}+1$ and $AB = \sin{\theta}$

4. From Pythagoras' theorem have that $CB^2 + AB^2 = CA^2$,
so $(\cos{\theta}+1)^2 + \sin^2{\theta} = 4 \cos^2{\frac{\theta}{2}}$
5. Substituting $\sin^2{\theta} = 1-\cos^2{\theta}$ and rearranging gives:
$(\cos{\theta}+1)^2+(1-\cos^2{\theta}) = 4\cos^2{\frac{\theta}{2}}$
$cos^2{\theta}+2\cos{\theta}+1+1-\cos^2{\theta}=4\cos^2{\frac{\theta}{2}}$
$2 \cos{\theta}+2 = 4\cos^2{\frac{\theta}{2}}$
$\cos^2{\frac{\theta}{2}}=\frac{1}{2}(\cos{\theta}+1)$
Yet another way to complete this proof after point 3 without using pythagoras could be to look at the expression for $\cos{\frac{\theta}{2}}$ in the triangle $ACB$.
You may also like
Powerful Quadratics
This comes in two parts, with the first being less fiendish than the second. It’s great for practising both quadratics and laws of indices, and you can get a lot from making sure that you find all the solutions. For a real challenge (requiring a bit more knowledge), you could consider finding the complex solutions.
Discriminating
You're invited to decide whether statements about the number of solutions of a quadratic equation are always, sometimes or never true.
Factorisable Quadratics
This will encourage you to think about whether all quadratics can be factorised and to develop a better understanding of the effect that changing the coefficients has on the factorised form.

