A4 Fraction Subtraction

A4 Fraction Subtraction

Find a partner and start with a sheet of A4 paper and a pair of scissors each. Have a go at the activity below and compare what you've made!

The whole sheet of A4 paper represents 1 whole.

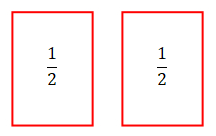
Take your sheet of paper and fold it in half into two rectangles. Unfold it and cut along the fold line. You might end up with two pieces which look like the two red rectangles below. Each of these rectangles represents $\frac{1}{2}$.

  

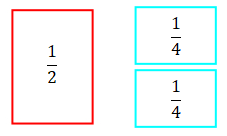
Take one of your rectangles and cut it in half into two smaller rectangles in the same way. By halving this you now have two rectangles which each represent $\frac{1}{4}$, like the blue rectangles below:

   

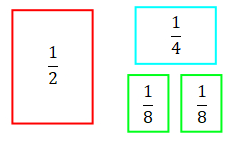
Now, take one of your $\frac{1}{4}$ rectangles and cut it in half. You will then have two new rectangles which both represent $\frac{1}{8}$ like the green rectangles below.

  

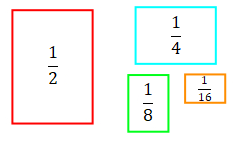
Halve one of your green rectangles to get two $\frac{1}{16}$ rectangles like the orange one below. Then throw away one of these$\frac{1}{16}$ rectangles so that you have one rectangle of each size.

  

 

You might have rectangles that look slightly different to these, depending on how you cut your rectangles!

Now, one person needs to get four pieces of A4 paper and attach one to each of their fraction pieces. Remember that the full piece of A4 paper is counted as "one whole".

You should end up with combinations that look a bit like the ones below. These are mixed numbers of pieces of A4 paper now, because they have a whole number part and a fraction part.

 

 

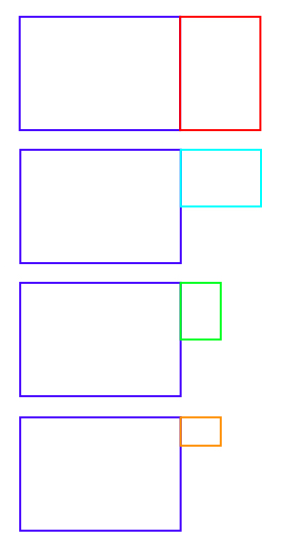
Can you work out which mixed number is represented by each?

The other person needs two new pieces of A4 paper so that they can make the following mixed numbers:

 
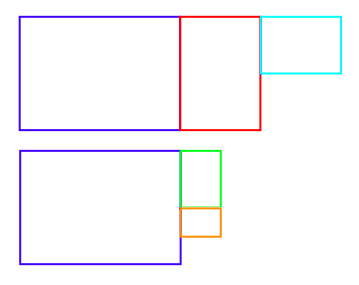
Can you work out what these shapes represent?

Take two sheets of A4 paper and put them together, like this:

 

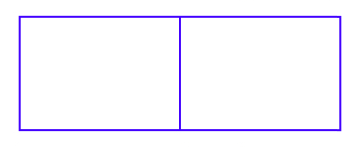
This rectangle now represents the number 2, as there are two wholes.

We are going to subtract our mixed numbers from this. Put one of your mixed numbers on top of the two sheets, and write the subtraction calculation. 

For example, the subtraction below would give you 2 - 1$\frac{1}{2}$ = $\frac{1}{2}$, because putting the 1$\frac{1}{2}$ shape over the 2 rectangle leaves a gap of $\frac{1}{2}$.

  

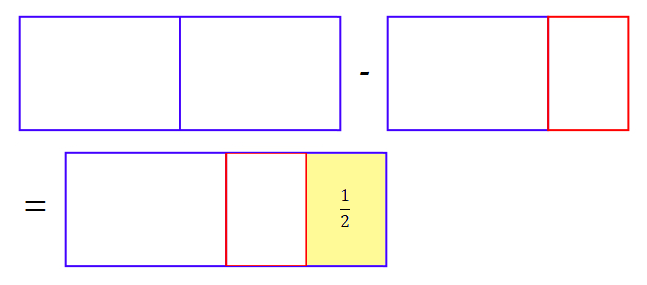
How many different subtraction number sentences can you make if you always subtract from 2?
 

You might also like to try an addition version of this task.

Why do this activity

This activity enables pupils to help to develop their concept of fractions and begin to subtract fractions with the same denominator and denominators that are multiples of the same number. It provides a context within which pupils can explore and reason about properties of fractions.

Possible approach

Begin with a large piece of paper and split this into fractions by repeated halving (as in the first part of the activity). Discuss with pupils the size of the pieces that you're making. Ask children to suggest how you could split the paper in half into two rectangles - there are two ways of doing this at each stage! Stick some of the parts to a fresh piece of paper (as in the second part of the activity) and ask them to describe what each is (1$\frac{1}{2}$, 1$\frac{1}{4}$, 1$\frac{1}{8}$ and 1$\frac{1}{16}$).

Working in pairs, pupils can then repeat the activity with their own pieces of paper. Then set them the task of doing the additions using their fractions, and recording as many number sentences as they can.

Key questions

Tell me about the size of this rectangle.
How are you subtracting these two?
How do you know that your solutions are correct?
Could you have chosen a different rectangle to represent that fraction?
Are there other ways of subtracting them?

Possible extension

When pupils have made the 1$\frac{1}{2}$, 1$\frac{1}{4}$, 1$\frac{1}{8}$ and 1$\frac{1}{16}$, they can then make 1$\frac{3}{4}$, 1$\frac{3}{8}$ and 1$\frac{3}{16}$. Then children can see how many subtraction number sentences they can make including those. They could also create different representations for the same subtraction, choosing differently shaped rectangles that represent the same fraction.

Possible support

Pupils could cut the fractions out of a sheet with the lines already marked (word, pdf).