Skip over navigation
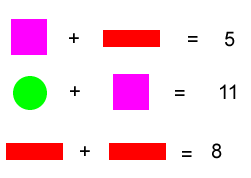



Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Shape Products
Age 11 to 14
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Why do this problem?
This problem helps students become familiar with the idea of a symbol (in this case a shape) representing a number. They will need to work systematically and use their knowledge of multiplication and division in order to solve the problem.
Possible approach
These printable resources may be useful: Shape ProductsIn order to introduce the idea of a shape representing a number, you could start the lesson by having some shapes representing numbers in addition sums. For example:
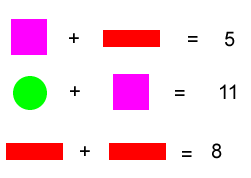
Ask students to talk to each other about how they would work out what each shape stands for in the calculations above, and then ask them to share their strategies. In this case the last sum is actually the most helpful to start with.
You could then display the first of these slides and explain the task. Ask the students to think on their own about where they might start. Invite them to share their ideas with a partner and work together using the worksheet. If they need some
more clues, the Support worksheet has four extra clues - these are also available on the second slide.
Once students have finished, challenge them to tackle the extension questions on the sheet. In a final plenary, discuss the strategies that students used to work out the value of each shape, and the order in which they used the different clues.
Key questions
What is special about clues C and D?
What is unusual about clues F and H?
What is unusual about clues F and H?
Possible extension
The problems Cryptarithms and What's it Worth? require similar thinking processes to this problem and would be good ones for students to try next.
Possible support
Students could prepare for this activity by initially tackling Missing Multipliers.
It may be appropriate for some students to start this activity with the Support worksheet with all 12 clues. Some students may like to cut out the 12 clues and move them around in order to more easily compare pairs that contain the same shape.
It may be appropriate for some students to start this activity with the Support worksheet with all 12 clues. Some students may like to cut out the 12 clues and move them around in order to more easily compare pairs that contain the same shape.
You may also like
Think of Two Numbers
Think of two whole numbers under 10, and follow the steps. I can work out both your numbers very quickly. How?
Special Numbers
My two digit number is special because adding the sum of its digits to the product of its digits gives me my original number. What could my number be?
Your Number Is...
Think of a number and follow the machine's instructions... I know what your number is! Can you explain how I know?

