Skip over navigation
Thank you very much to Pablo and Sergio from King's College Alicante in Spain, Z. Hakim from Annie Gale Jr High in Canada and Michele from Hockerill Anglo-European College in Italy, who all sent in good work on this problem. The solution below draws on their observations and explanations.
Multiplying by a real number
Here are some examples of multiplying a complex number by a positive real number:
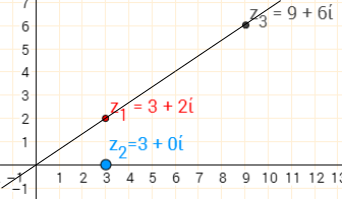 $(3+2i)\times(3+0i)=9+6i$
$(3+2i)\times(3+0i)=9+6i$
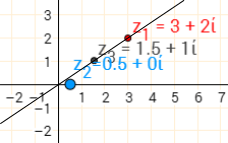 $(3+2i)\times(0.5+0i)=1.5+i$
$(3+2i)\times(0.5+0i)=1.5+i$
Multiplying $z_1$ by a real number $z_2$ enlarges $z_1$ by a scale factor of $z_2$, centred at $0+0i$.
The same happens if $z_2$ is negative, but this time the scale factor is negative, so $z_3$ is on the other side of $0+0i$:
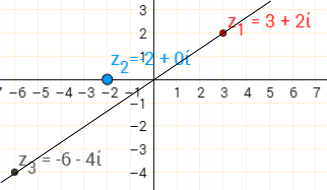 $(3+2i)\times(-2+0i)=-6-4i$
$(3+2i)\times(-2+0i)=-6-4i$
Multiplying by $i$
Some examples are shown below. To help see the effect, the line segments joining $z_1$ and $z_3$ to $0+0i$ are also shown, and the right-angled triangles that these make with the axes are shaded.
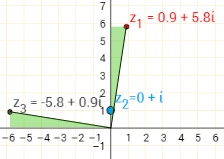 $(0.9+5.8i) i=-5.8+0.9i$
$(0.9+5.8i) i=-5.8+0.9i$
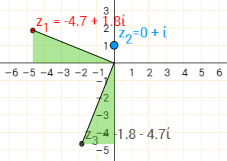 $(-4.7+1.8i) i=-1.8-4.7i$
$(-4.7+1.8i) i=-1.8-4.7i$
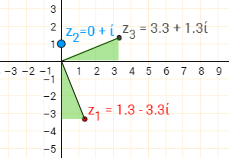 $(1.3-3.3i) i=3.3+1.3i$
$(1.3-3.3i) i=3.3+1.3i$
Since in each case, the vertical side of one green triangle is equal to the horizontal side of the other and vice versa, the triangles must be congruent. So the distance from $0+0i$ to $z_3$ is the same as the distance from $0+0i$ to $z_1$. Also, the angle at $0+0i$ is the same in each pair of triangles, so the angles between their hypotensues must be $90^\circ$, the same as the angle between the real and imaginary axes.
So in each case, multiplication by $i$ represents a rotation of $90^\text o$ anticlockwise about $0+0i$.
We can use Pythagoras' Theorem to prove that the distance from $0+0i$ does not change.
e.g. For the first pair:
The distance of both $z_1$ and $z_3$ from $0+0i$ is $\sqrt{0.9^2+5.8^2}$.
We can use the gradients of the lines joining $z_1$ and $z_3$ to $0+0i$ to prove that they are perpendicular.
e.g. For the first pair:
The lines have gradients $\frac{5.8}{0.9}$ and $\frac{0.9}{-5.8}$
$\frac{5.8}{0.9}\times\frac{0.9}{-5.8}=-1$ so the lines are perpendicular.
We can also do this for a general complex number $z_1 = a+bi$:
$$z_3 = (a+bi)\times i=ai+bi^2=-b+ai$$
The distance of both $z_1$ and $z_3$ from $0+0i$ is $\sqrt{a^2+b^2}$
The gradients of the line segments joining $z_1$ and $z_3$ to $0+0i$ are $\frac ba$ and $\frac{a}{-b}$
$\frac ba\times\frac a{-b}=-1$, so they are perpendicular.
Multiplying by a multiple of $i$
Some examples are shown below.
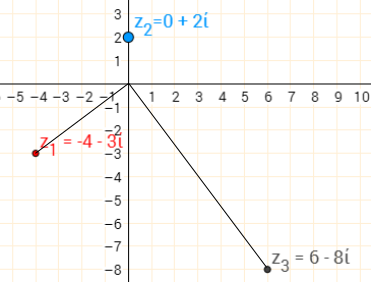 $(-4-3i)\times(0+2i)=6-8i$
$(-4-3i)\times(0+2i)=6-8i$
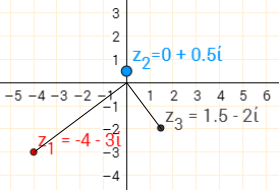 $(-4-3i)\times(0+0.5i)=1.5-2i$
$(-4-3i)\times(0+0.5i)=1.5-2i$
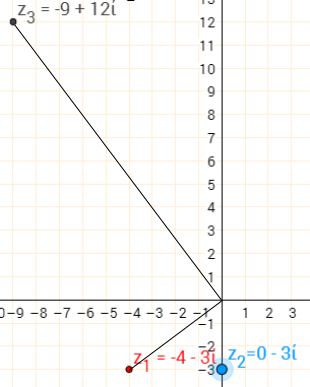 $(-4-3i)\times(-3i)=12+9i$
$(-4-3i)\times(-3i)=12+9i$
The angle between the lines joining $z_1$ and $z_3$ to $0+0i$ are still perpendicular, so there is still a rotation of $90^\text o$ about $0+0i$. Notice that this rotation appears to be anticlockwise when $z_2$ is $2i$ or $0.5i$, but clockwise when $z_2=-3i$. So if $b$ is negative, then the direction of the rotation is reversed.
Also notice that $z_3$ is either closer to, or further from, $0+0i$ than $z_1$ is. So as well as a rotation, there is an enlargement centred at the origin. The scale factor of the enlargement is the size of $b$ - so when $b=2$ the scale factor is $2$, and when $b=-3$, the scale factor is $3$.
For positive values of $b$, this agrees with what we had seen so far, since multiplying by $bi$ is the same as multiplying by $i$ (rotation) and by $b$ (enlargement).
For negative values of $b$, we have said that the rotation is clockwise instead of anticlockise. We could explain this by saying that the enlargement has a negative scale factor, so everything is moved to the other side of the origin, which has the same effect as changing the direction of the rotation.


Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Strolling Along
Age 14 to 18
Challenge Level 





- Problem
- Student Solutions
Thank you very much to Pablo and Sergio from King's College Alicante in Spain, Z. Hakim from Annie Gale Jr High in Canada and Michele from Hockerill Anglo-European College in Italy, who all sent in good work on this problem. The solution below draws on their observations and explanations.
Multiplying by a real number
Here are some examples of multiplying a complex number by a positive real number:
 $(3+2i)\times(3+0i)=9+6i$
$(3+2i)\times(3+0i)=9+6i$ $(3+2i)\times(0.5+0i)=1.5+i$
$(3+2i)\times(0.5+0i)=1.5+i$Multiplying $z_1$ by a real number $z_2$ enlarges $z_1$ by a scale factor of $z_2$, centred at $0+0i$.
The same happens if $z_2$ is negative, but this time the scale factor is negative, so $z_3$ is on the other side of $0+0i$:
 $(3+2i)\times(-2+0i)=-6-4i$
$(3+2i)\times(-2+0i)=-6-4i$Multiplying by $i$
Some examples are shown below. To help see the effect, the line segments joining $z_1$ and $z_3$ to $0+0i$ are also shown, and the right-angled triangles that these make with the axes are shaded.
 $(0.9+5.8i) i=-5.8+0.9i$
$(0.9+5.8i) i=-5.8+0.9i$ $(-4.7+1.8i) i=-1.8-4.7i$
$(-4.7+1.8i) i=-1.8-4.7i$ $(1.3-3.3i) i=3.3+1.3i$
$(1.3-3.3i) i=3.3+1.3i$Since in each case, the vertical side of one green triangle is equal to the horizontal side of the other and vice versa, the triangles must be congruent. So the distance from $0+0i$ to $z_3$ is the same as the distance from $0+0i$ to $z_1$. Also, the angle at $0+0i$ is the same in each pair of triangles, so the angles between their hypotensues must be $90^\circ$, the same as the angle between the real and imaginary axes.
So in each case, multiplication by $i$ represents a rotation of $90^\text o$ anticlockwise about $0+0i$.
We can use Pythagoras' Theorem to prove that the distance from $0+0i$ does not change.
e.g. For the first pair:
The distance of both $z_1$ and $z_3$ from $0+0i$ is $\sqrt{0.9^2+5.8^2}$.
We can use the gradients of the lines joining $z_1$ and $z_3$ to $0+0i$ to prove that they are perpendicular.
e.g. For the first pair:
The lines have gradients $\frac{5.8}{0.9}$ and $\frac{0.9}{-5.8}$
$\frac{5.8}{0.9}\times\frac{0.9}{-5.8}=-1$ so the lines are perpendicular.
We can also do this for a general complex number $z_1 = a+bi$:
$$z_3 = (a+bi)\times i=ai+bi^2=-b+ai$$
The distance of both $z_1$ and $z_3$ from $0+0i$ is $\sqrt{a^2+b^2}$
The gradients of the line segments joining $z_1$ and $z_3$ to $0+0i$ are $\frac ba$ and $\frac{a}{-b}$
$\frac ba\times\frac a{-b}=-1$, so they are perpendicular.
Multiplying by a multiple of $i$
Some examples are shown below.
 $(-4-3i)\times(0+2i)=6-8i$
$(-4-3i)\times(0+2i)=6-8i$ $(-4-3i)\times(0+0.5i)=1.5-2i$
$(-4-3i)\times(0+0.5i)=1.5-2i$ $(-4-3i)\times(-3i)=12+9i$
$(-4-3i)\times(-3i)=12+9i$The angle between the lines joining $z_1$ and $z_3$ to $0+0i$ are still perpendicular, so there is still a rotation of $90^\text o$ about $0+0i$. Notice that this rotation appears to be anticlockwise when $z_2$ is $2i$ or $0.5i$, but clockwise when $z_2=-3i$. So if $b$ is negative, then the direction of the rotation is reversed.
Also notice that $z_3$ is either closer to, or further from, $0+0i$ than $z_1$ is. So as well as a rotation, there is an enlargement centred at the origin. The scale factor of the enlargement is the size of $b$ - so when $b=2$ the scale factor is $2$, and when $b=-3$, the scale factor is $3$.
For positive values of $b$, this agrees with what we had seen so far, since multiplying by $bi$ is the same as multiplying by $i$ (rotation) and by $b$ (enlargement).
For negative values of $b$, we have said that the rotation is clockwise instead of anticlockise. We could explain this by saying that the enlargement has a negative scale factor, so everything is moved to the other side of the origin, which has the same effect as changing the direction of the rotation.
You may also like
Roots and Coefficients
If xyz = 1 and x+y+z =1/x + 1/y + 1/z show that at least one of these numbers must be 1. Now for the complexity! When are the other numbers real and when are they complex?
Target Six
Show that x = 1 is a solution of the equation x^(3/2) - 8x^(-3/2) = 7 and find all other solutions.
8 Methods for Three by One
This problem in geometry has been solved in no less than EIGHT ways by a pair of students. How would you solve it? How many of their solutions can you follow? How are they the same or different? Which do you like best?

