Skip over navigation
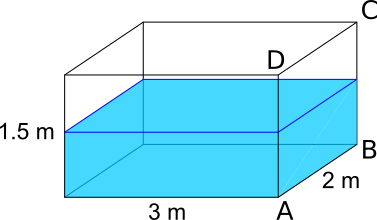The rectangular base of an aquarium is 2 metres by 3 metres, and its height is 1.5 metres. The aquarium is tilted along AB (so that the side AB is still along the floor) until the water completely covers the face ABCD. At this point, it also covers 80% of the 2 by 3 metre base.
What is the depth of the water when the aquarium is level?
This problem is adapted from the World Mathematics Championships
Tilted Aquarium
Age 14 to 16
ShortChallenge Level 
The rectangular base of an aquarium is 2 metres by 3 metres, and its height is 1.5 metres. The aquarium is tilted along AB (so that the side AB is still along the floor) until the water completely covers the face ABCD. At this point, it also covers 80% of the 2 by 3 metre base.
What is the depth of the water when the aquarium is level?
This problem is adapted from the World Mathematics Championships
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Dividing the Field
A farmer has a field which is the shape of a trapezium as illustrated below. To increase his profits he wishes to grow two different crops. To do this he would like to divide the field into two trapeziums each of equal area. How could he do this?
Two Circles
Draw two circles, each of radius 1 unit, so that each circle goes through the centre of the other one. What is the area of the overlap?
Star Gazing
Find the ratio of the outer shaded area to the inner area for a six pointed star and an eight pointed star.