Finding 3D Stacks
Finding 3D Stacks
This activity may be used as a follow-on for those who have successfully worked at Doplication.
Let me help you visualise this representation of a 3D situation.
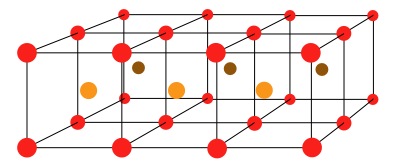
The picture below shows a 2 by 3 by 4 arrangement of red spheres, which you might see as two layers of 3 by 4:
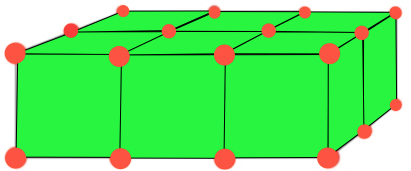
These two layers together could also be viewed as representing six cubes:
How did you count them?
Use your system of counting to find the total number of spheres for other sizes, for example 3 by 3 by 3; 3 by 4 by 4; 4 by 4 by 5 etc.
How would you find the number of spheres for any sized arrangement?
Why do this problem?
Possible approach
You could show the group the images in the problem and invite them to 'say what they see'. Facilitate discussion amongst learners so that the structure of the arrangement is clear.
Ask learners to work on the questions in pairs and then bring them together at a suitable point to check that everyone agrees with the total number of spheres. Encourage them to articulate how they are going about counting and record the different ways on the board for all to see. (Pairs may then stick with their own approach or adopt someone else's.)
Once they have had the opportunity to count several examples (a spreadsheet might be useful for recording these), challenge pupils to move from the particular to the general. Give them time to compose instructions for counting the spheres for any size grid. Once language-based instructions have been created, help them move to a formula. Depending on the children's experience, you could do
this as a whole group by choosing one method and working on it together.
Key questions
Possible extension
Learners could compare the 3 by 3 by 3 arrangement of this challenge with the 3 by 3 of Doplication; then the 4 by 4 and 5 by 5 and so on.
Possible support
The visualisation may be difficult for some so using construction materials may be helpful.
You may also like
Counting Counters
Take a counter and surround it by a ring of other counters that MUST touch two others. How many are needed?
Cuisenaire Squares
These squares have been made from Cuisenaire rods. Can you describe the pattern? What would the next square look like?
Doplication
We can arrange dots in a similar way to the 5 on a dice and they usually sit quite well into a rectangular shape. How many altogether in this 3 by 5? What happens for other sizes?