Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Price Match



- Problem
- Getting Started
- Teachers' Resources
Price Match
You might like to try Through the Window before this challenge.
”‹In a particular shop, the price of windows is calculated according to the area of glass used and the length of frame needed.
In the picture below, glass costs £10 for an area of one small square, plus £5 for every square edge of frame.
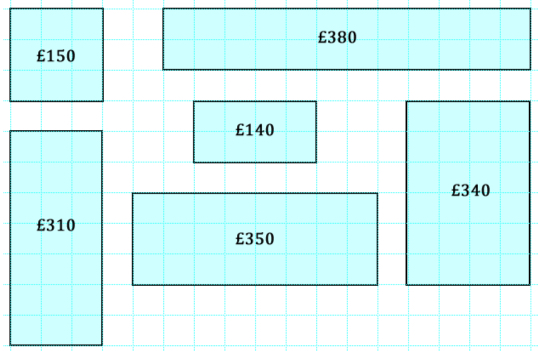
If we call the area of the glass A and the perimeter of the window P, how would you express the cost of the window in terms of A and P?
Use your formula to find pairs of rectangular windows that are different sizes but cost the same.
Why do this activity?
This activity would make a good introduction to creating and using formula. It can be approached in a variety of ways, depending on the experience of the learners, and does not necessarily require an ability to manipulate expressions algebraically. It lends itself to a combination of trial and improvement, and working systematically.
Possible approach
It would be worth projecting the image for the group to see and sharing the information about how the cost of windows is calculated. Give learners some time (in pairs) to check that they understand the pricing structure, perhaps by testing that a few of the windows are priced correctly.
Invite some pairs to share how they went about this checking process and then introduce the challenge of finding a formula to express the total cost. You may find that some pairs have already generalised in this way so it could be a case of building on some contributions and working on this part of the problem as a whole group. (It is not necessary that every pair has expressed the
formula in exactly the same way, but you may want to have a conversation about how we know they are equivalent.)
The main part of the task might be best tackled in small groups. You could have a mini plenary after a short time to share ways of working and you may find that some groups adopt different approaches as a result.
The problem does not specifically ask learners to find all the pairs of windows which have the same cost but a plenary could focus on how you could guarantee that you do not miss any solutions.
Key questions
How did you go about this part of the task?
Tell me about your solutions.
How will you remember what you have found out so far?
Possible extension
Pupils who are confident could create another similar challenge of their own for others to do.Possible support
There may be a need for some equipment to help support the emerging thinking. Some may need to be directed to squared paper as an aid.You may also like
Your Number Is...
Think of a number and follow the machine's instructions... I know what your number is! Can you explain how I know?
Diagonal Sums
In this 100 square, look at the green square which contains the numbers 2, 3, 12 and 13. What is the sum of the numbers that are diagonally opposite each other? What do you notice?

